Tìm a thuộc Z để ( 2 .a2 + 12 ) chia hết ( a2 + 1 )
Những câu hỏi liên quan
Bài 1:Cho a1,a2,....,a2018 thuộc ZCMR:a1+a2+...+a2018 chia hết cho 30 khi và chỉ khi a1^5 + a2^5 +...+ a2018^5 chia hết cho 30Bài 2: Tìm x,y thuộc N* sao cho x+y+1 chia hết cho xyBài 3: tìm x,y thuộc N* sao cho y+1 chia hết cho x, x+1 chia hết cho yBài 4:Tìm x,y thuộc N* sao cho y+2 chia hết cho x, x+2 chia hết cho yBài 5: Tìm x,y thuộc N* sao cho 2x+1 chia hết cho y, 2y+1 chia hết cho xBài 6: CMR: Với mọi n thuộc Z ta có n^5 + 5n chia hết cho 6Bài 7:CMR: Với mọi n thuộc Z ta có n(2n+7)(7n+1) ch...
Đọc tiếp
Bài 1:Cho a1,a2,....,a2018 thuộc Z
CMR:a1+a2+...+a2018 chia hết cho 30 khi và chỉ khi a1^5 + a2^5 +...+ a2018^5 chia hết cho 30\
Bài 2: Tìm x,y thuộc N* sao cho x+y+1 chia hết cho xy
Bài 3: tìm x,y thuộc N* sao cho y+1 chia hết cho x, x+1 chia hết cho y
Bài 4:Tìm x,y thuộc N* sao cho y+2 chia hết cho x, x+2 chia hết cho y
Bài 5: Tìm x,y thuộc N* sao cho 2x+1 chia hết cho y, 2y+1 chia hết cho x
Bài 6: CMR: Với mọi n thuộc Z ta có n^5 + 5n chia hết cho 6
Bài 7:CMR: Với mọi n thuộc Z ta có n(2n+7)(7n+1) chia hết cho 6
Giúp mình nhé, cảm ơn các bạn nhiều!!!
6 \(n^5+5n=n^5-n+6n=n\left(n^4-1\right)+6n=n\left(n^2-1\right)\left(n^2+1\right)+6n\)
\(=n\left(n-1\right)\left(n+1\right)\left(n^2+1\right)+6n\)
vì n,n-1 là 2 số nguyên lien tiếp \(\Rightarrow n\left(n-1\right)⋮2\Rightarrow n\left(n-1\right)\left(n+1\right)\left(n^2+1\right)⋮2\)
n,n-1,n+1 là 3 sô nguyên liên tiếp \(\Rightarrow n\left(n-1\right)\left(n+1\right)⋮3\Rightarrow n\left(n-1\right)\left(n+1\right)\left(n^2+1\right)⋮3\)
\(\Rightarrow n\left(n-1\right)\left(n+1\right)\left(n^2+1\right)⋮2\cdot3=6\)
\(6⋮6\Rightarrow6n⋮6\Rightarrow n\left(n-1\right)\left(n+1\right)\left(n^2+1\right)-6n⋮6\Rightarrow n^5+5n⋮6\)(đpcm)
7 \(n\left(2n+7\right)\left(7n+1\right)=n\left(2n+7\right)\left(7n+7-6\right)=7n\left(n+1\right)\left(2n+7\right)-6n\left(2n+7\right)\)
\(=7n\left(n+1\right)\left(2n+4+3\right)-6n\left(2n+7\right)\)
\(=7n\left(n+1\right)\left(2n+4\right)+21n\left(n+1\right)-6n\left(2n+7\right)\)
\(=14n\left(n+1\right)\left(n+2\right)+21n\left(n+1\right)-6n\left(2n+7\right)\)
n,n+1,n+2 là 3 sô nguyên liên tiếp dựa vào bài 6 \(\Rightarrow n\left(n+1\right)\left(n+2\right)⋮6\Rightarrow14n\left(n+1\right)\left(n+2\right)⋮6\)
\(21⋮3;n\left(n+1\right)⋮2\Rightarrow21n\left(n+1\right)⋮3\cdot2=6\)
\(6⋮6\Rightarrow6n\left(2n+7\right)⋮6\)
\(\Rightarrow14n\left(n+1\right)\left(n+2\right)+21n\left(n+1\right)-6n\left(2n+7\right)⋮6\)
\(\Rightarrow n\left(2n+7\right)\left(7n+1\right)⋮6\)(đpcm)
Đúng 0
Bình luận (0)
......................?
mik ko biết
mong bn thông cảm
nha ................
Đúng 0
Bình luận (0)
BAI1 Chứng minh rằng với a1,a2,.....,an thuộc Z
Nếu a1<a2,a2<a3,..........an-1<a thì a1<an
BAI2 a, Tìm x thuộc Z biết/x/=-2003, /x/ = /-2003/
b,Tìm x thuộc Z để / x/ +2003 đạt giá trị nhỏ nhất
c,Tìm x,y thuộc Z, biêt /x/+/y/ nhỏ hơn hoặc bằng 0
bạn đã k đủ 3k hẹn lần sau
Bai 1. tinh chat bac cau
bai 2> a) x=+-2003
b) >x=0
c)x=y=0
Đúng 0
Bình luận (0)
1)a)tìm n thuộc N*để 3n+1chia hết cho5n-2b)tìm các chữ số a,,b,c để 7268abc chia hết cho 7,12,8,92)cho a và blaf 2 số nguyên tố cùng nhau sao cho a,b khác tính chẵn lẻ cmr a+b và a(a+2)+ab là 2 số nguyên tố cùng nhau3)cmr với mọi n thuộc N* thì1.2.3+2.3.5+3.4.7+..+n(n+1)(2n+1)n(n+1)^2(n+2)/24)cho 17 số tự nhiên khác 0:a1,a2,a3,....,a17mà a1+a2+a3+...+a17153153cmr a1^5+a2^9+a3^13+...+a17^69 không phải số chính phương
Đọc tiếp
1)a)tìm n thuộc N*để 3n+1chia hết cho5n-2
b)tìm các chữ số a,,b,c để 7268abc chia hết cho 7,12,8,9
2)cho a và blaf 2 số nguyên tố cùng nhau sao cho a,b khác tính chẵn lẻ cmr a+b và a(a+2)+ab là 2 số nguyên tố cùng nhau
3)cmr với mọi n thuộc N* thì
1.2.3+2.3.5+3.4.7+..+n(n+1)(2n+1)=n(n+1)^2(n+2)/2
4)cho 17 số tự nhiên khác 0:a1,a2,a3,....,a17mà a1+a2+a3+...+a17=153153
cmr a1^5+a2^9+a3^13+...+a17^69 không phải số chính phương
ai muốn kết bn với tớ thì hãy click cho tớ nhé
Đúng 0
Bình luận (0)
Tìm a thuoc Z biết : a2 + 5 chia het a2 + 2
a^2 + 5 =( a^2+2) +3
t cos ( a^2+2) chia heetsc cho a^2+2
=> 3 phai chia hết cho a^2+2
=> mà đến mình ko biết a^2 hay là 2a
SỬa đi mk làm cho
Đề bài:
Tìm a thuộc Z:a.2 + 5 chia hết cho a.2 + 2 nha!!!
a) Chứng minh rằng: a3- a chia hết cho 6 với mọi giá trị a thuộc Z
b)Cho a,b,c thuộc Z thỏa mãn: a+b+c= 450 mũ 2023. Chứng minh rằng: a2+b2+c2 chia hết cho 6
a: a^3-a=a(a^2-1)
=a(a-1)(a+1)
Vì a;a-1;a+1 là ba số liên tiếp
nên a(a-1)(a+1) chia hết cho 3!=6
=>a^3-a chia hết cho 6
Đúng 0
Bình luận (0)
Bài 1 : Tìm các số nguyên a , b biết tích của chúng là 24 và tổng của 2 số đó là - 40
Bài 2 : CMR với mọi số nguyên a ta có ( a - 1 ) * ( a + 2 ) +12 không chia hết cho 9 và không là bội của 9
Bài 3 : Cho dãy a1 ; a2 ; a3 ; ... ; a160 . Trong đó a1 = 1 ; a2 = -1 ; ak = ak - 2 * ak - 1 ( K thuộc số tự nhiên ; K nhỏ hơn hoặc bằng 3 ) . Tính a100
12 tháng 9 2021 lúc 13:57
Tìm chữ số tận cùng của số tự nhiên a để có a2 + 1 chia hết cho 5.
Ta có: \(a^2+1⋮5\)
\(\Rightarrow a^2\) có tận cùng là 4 hoặc 9
Vậy a có tận cùng là 2 hoặc 3
Đúng 1
Bình luận (0)
Tập hợp A{0,1,2,3,4,5,6,7}; E{
a
1
a
2
a
3
a
4
¯
/
a
1
,
a
2
,
a
3
,
a
4
...
Đọc tiếp
Tập hợp A={0,1,2,3,4,5,6,7}; E={ a 1 a 2 a 3 a 4 ¯ / a 1 , a 2 , a 3 , a 4 ∈ A , a 1 ≠ 0 }
Lấy 1 phần tử thuộc E bất kỳ. Tính xác suất để số đó chia hết cho 5
A. 
B. 
C. 
D. 
Đáp án D
Số phần tử của tập 
Để 
chia hết cho 5 điều kiện cần và đủ là 
hay 
Nếu 
thì lấy trong 7 chữ số 1,2,...,7
Vậy có 
số tận cùng bằng 0
Nếu 
thì các số 
là 
số
Vây xác suất để số đó chia hết cho 5 là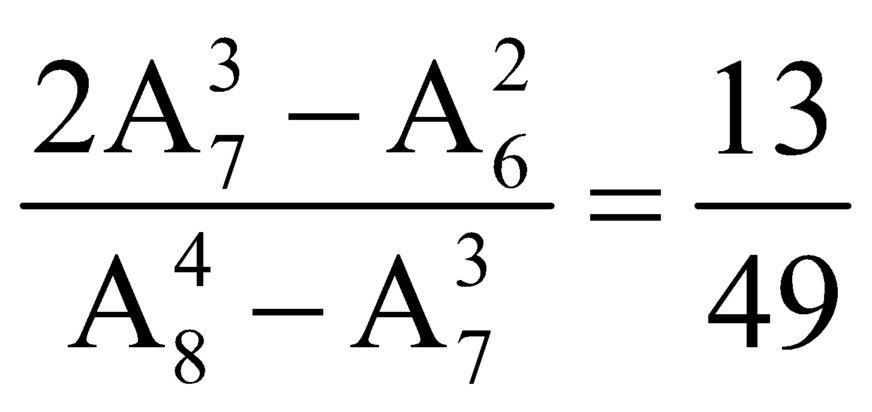 
Đúng 0
Bình luận (0)
Tập hợp
A
0
;
1
;
2
;
3
;
4
;
5
;
6
;
7
,
E
a
1
a
2
a
3
a
4
/
a
1
;
a...
Đọc tiếp
Tập hợp A = 0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 , E = a 1 a 2 a 3 a 4 / a 1 ; a 2 ; a 3 ; a 4 ∈ A , a 1 ≠ 0 . Lấy 1 phần tử thuộc E bất kỳ. Tính xác suất để số đó chia hết cho 5
A. 5/16
B. 13/98
C. 1/4
D. 13/49
giúp mình với cho a1,a2,a3,...,an\(\in\)Z CMR a1^5+a2^5+...+an^5 chia hết cho 30 <=> a1+a2+...+an chia hết cho 30>>help me