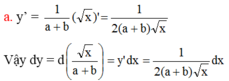tìm các hằng số a;b sao cho x3+ã +b chia cho x+1 dư 7 chia cho x+2 dư 4

Những câu hỏi liên quan
Tìm vi phân của các hàm số sau: y = x a + b (a,b là các hằng số)
Cho a, b là các hằng số . Tìm các biến trong biểu thức đại số x ( a 2 - a b + b 2 + y )
A. a, b
B. a, b, x, y
C. x, y
D. a, b, x
Biểu thức x ( a 2 - a b + b 2 + y ) có các biến là x, y
Chọn đáp án C
Đúng 0
Bình luận (0)
Tìm bậc của các đa thức ax³-2x³+x(a là hằng số)
\(ax^3-2x^3+x=\left(a-2\right)x^3+x\)
- Với \(a=2\Rightarrow\) đa thức trở thành \(x\) có bậc 1
- Với \(a\ne2\Rightarrow\) đa thức có bậc 3
Vậy đa thức có bậc 1 nếu \(a=2\) và có bậc 3 nếu \(a\ne2\)
Đúng 2
Bình luận (0)
1. tìm các hằng số a và b sao cho x^3 + ax + b chia hết cho x+1 thì dư 7 chia cho x-3 dư -5.
2. tìm các hằng số a,b,c sao cho ax^3 + bx^2 + c chia cho x+ 2 , chia cho x^2 - 1 thì dư x+5
Dựa vào vị trí tương đối giữa hai đường thẳng dưới đây, hãy tìm mối liên hệ giữa các hằng số a, b, c và các hằng số a’, b’, c’ để hệ phương trình
a
x
+
b
y
c
a
x...
Đọc tiếp
Dựa vào vị trí tương đối giữa hai đường thẳng dưới đây, hãy tìm mối liên hệ giữa các hằng số a, b, c và các hằng số a’, b’, c’ để hệ phương trình a x + b y = c a ' x + b ' y = c '
Có vô số nghiệm
Áp dụng:
Lập một hệ hai phương trình bậc nhất hai ẩn có vô số nghiệm.
Xét các trường hợp:
1. a, b, a’, b’ ≠ 0
Ta có:
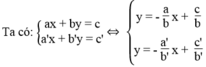
Hệ phương trình có vô số nghiệm khi hai đường thẳng trùng nhau. Nghĩa là hai đường thẳng có hệ số góc và tung độ gốc bằng nhau:
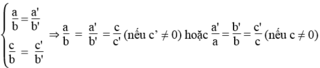
*a = 0, a’ ≠ 0
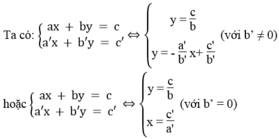
Vì hai đường thẳng 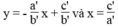 luôn luôn cắt trục hoành còn đường thẳng y = c/b song song hoặc trùng với trục hoành nên chúng luôn luôn cắt nhau.
luôn luôn cắt trục hoành còn đường thẳng y = c/b song song hoặc trùng với trục hoành nên chúng luôn luôn cắt nhau.
Vậy hệ phương trình chỉ có một nghiệm duy nhất.
*a = a’ = 0
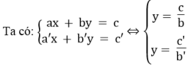
Hệ có vô số nghiệm khi hai đường thẳng trùng nhau, nghĩa là:
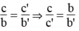
Hệ vô nghiệm khi hai đường thẳng song song nhau, nghĩa là:
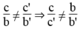
*b = 0, b’ ≠ 0
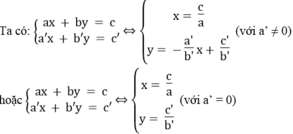
Vì hai đường thẳng 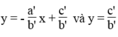 luôn luôn cắt trục tung còn đường thẳng x = c/a song song hoặc trùng với trục tung nên chúng luôn luôn cắt nhau.
luôn luôn cắt trục tung còn đường thẳng x = c/a song song hoặc trùng với trục tung nên chúng luôn luôn cắt nhau.
Vậy hệ phương trình chỉ có một nghiệm duy nhất.
*b = b’ = 0
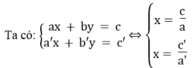
Hệ có vô số nghiệm khi hai đường thẳng trùng nhau, nghĩa là:
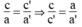
Hệ vô nghiệm khi hai đường thẳng song song nhau, nghĩa là:
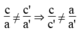
Áp dụng:
Hệ hai phương trình bậc nhất hai ẩn có vô số nghiệm:
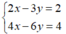
Vì 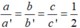 nên hệ phương trình có vô số nghiệm
nên hệ phương trình có vô số nghiệm
Đúng 0
Bình luận (0)
Dựa vào vị trí tương đối giữa hai đường thẳng dưới đây, hãy tìm mối liên hệ giữa các hằng số a, b, c và các hằng số a’, b’, c’ để hệ phương trình
a
x
+
b
y
c
a
x...
Đọc tiếp
Dựa vào vị trí tương đối giữa hai đường thẳng dưới đây, hãy tìm mối liên hệ giữa các hằng số a, b, c và các hằng số a’, b’, c’ để hệ phương trình a x + b y = c a ' x + b ' y = c '
Vô nghiệm
Áp dụng:
Lập một hệ hai phương trình bậc nhất hai ẩn vô nghiệm.
Xét các trường hợp:
1. a, b, a’, b’ ≠ 0
Ta có:
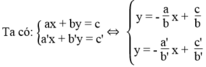
Hệ phương trình vô nghiệm khi hai đường thẳng song song nhau. Nghĩa là hai đường thẳng có hệ số góc bằng nhau và tung độ gốc khác nhau:
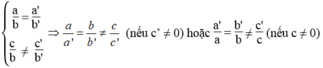
Áp dụng:
Hệ hai phương trình bậc nhất hai ẩn vô nghiệm:
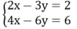
Vì 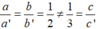 nên hệ phương trình trên vô nghiệm
nên hệ phương trình trên vô nghiệm
Đúng 0
Bình luận (0)
Tìm đa thức A và các hằng số a,b
A(7+4x-2x^2)=-7+ax+bx^2-2x^3
cho 1 số có 6 chữ số .Biết các chữ số hàng trăm ngàn,hàng ngàn,hằng trăm và hằng đơn vị lần lượt là 5,3,8,9.Hãy tìm các chữ số đó để để số đó chia cho 2,cho 3 và cho 5 đều dư1.Viết các số tìm được.
Dựa vào vị trí tương đối giữa hai đường thẳng dưới đây, hãy tìm mối liên hệ giữa các hằng số a, b, c và các hằng số a’, b’, c’ để hệ phương trình
a
x
+
b
y
c
a
x...
Đọc tiếp
Dựa vào vị trí tương đối giữa hai đường thẳng dưới đây, hãy tìm mối liên hệ giữa các hằng số a, b, c và các hằng số a’, b’, c’ để hệ phương trình a x + b y = c a ' x + b ' y = c '
Có nghiệm duy nhất
Áp dụng:
Lập một hệ hai phương trình bậc nhất hai ẩn có nghiệm duy nhất.
Xét các trường hợp:
1. a, b, a’, b’ ≠ 0
Ta có:
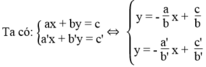
Hệ phương trình có một nghiệm duy nhất khi hai đường thẳng cắt nhau. Nghĩa là hai đường thẳng có hệ số góc khác nhau:
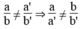
Áp dụng:
Hệ hai phương trình bậc nhất hai ẩn vô nghiệm:
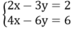
Vì 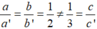 nên hệ phương trình trên vô nghiệm
nên hệ phương trình trên vô nghiệm
Đúng 0
Bình luận (0)
Tính các đơn thức rồi tìm bậc của đon thức thu được
(3a2x6y4).(-x2y2).(-2ay3z) (Với a là hằng số khác 0)
\(=3a^2x^6y^4\cdot x^2y^2\cdot2ay^3z=6a^3\cdot x^8y^9z\)
Bậc là 18
Đúng 1
Bình luận (0)
Ta có:(3a2x6y4).(-x2y2).(-2ay3z)
=(3\(a^2\).2a).(\(x^6.x^2\)).(\(y^4.y^2.y^3\)).z (với a là hằng số khác 0)
=6\(a^3x^8y^7z\)
Bậc của đơn thức là 8+7+1=16 (với a là hằng số khác 0)
Đúng 0
Bình luận (0)
Ta có:(3a2x6y4).(-x2y2).(-2ay3z)
=(3\(a^2\).2a).(\(x^6.x^2\)).(\(y^4.y^2.y^3\)).z (với a là hằng số khác 0)
=6\(a^3x^8y^9z\)
Bậc của đơn thức là 8+9+1=18 (với a là hằng số khác 0
Đúng 0
Bình luận (0)