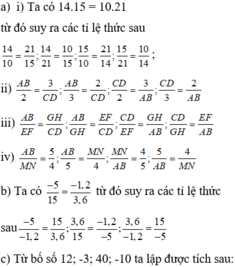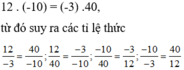Cho đẳng thức sau: 𝑥. 𝑦 = −2.3. Tỉ lệ thức nào đúng khi được suy ra từ đẳng thức đó.

Những câu hỏi liên quan
a/ Lập tất cả các tỉ lệ thức có thể được từ tỉ lệ thức 2 : 3 = 4 : 6
b/ Cho 𝑥/4=𝑦/7và xy = 112. Tìm x và y ?
\(a,\dfrac{2}{4}=\dfrac{3}{6};\dfrac{6}{4}=\dfrac{3}{2};\dfrac{2}{3}=\dfrac{4}{6};\dfrac{4}{3}=\dfrac{4}{2}\\ b,\text{Đặt }\dfrac{x}{4}=\dfrac{y}{7}=k\Rightarrow x=4k;y=7k\\ \text{Ta có }xy=112\\ \Rightarrow28k^2=112\\ \Rightarrow k^2=4\Rightarrow\left[{}\begin{matrix}k=2\\k=-2\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=8;y=14\\x=-8;y=-14\end{matrix}\right.\)
Đúng 0
Bình luận (0)
từ tỉ lệ thức có thể suy ra được tỉ lệ thức nào
Đọc tiếp
từ tỉ lệ thức  có thể suy ra được tỉ lệ thức nào
có thể suy ra được tỉ lệ thức nào
Chắc là \(\dfrac{a}{d}=\dfrac{c}{b}\)
Đúng 1
Bình luận (0)
từ tỉ lệ thức
\(\dfrac{a}{b}\)=\(\dfrac{c}{d}\)
có thể suy ra được tỉ lệ thức
a:b=c:d
Đúng 0
Bình luận (0)
Cho 𝑥, 𝑦, 𝑧,𝑡 ≠ 0 và 𝑥 + 𝑦 + 𝑧 + 𝑡 ≠ 0 thỏa mãn 𝑥 /𝑦 = 𝑦/ 𝑧 = 𝑧 /𝑡 = 𝑡/ 𝑥 Tính giá trị của biểu thức: M = 2𝑥−𝑦/ 𝑧+𝑡 + 2𝑦−𝑧/ 𝑡+𝑥 + 2𝑧−𝑡/ 𝑥+𝑦 + 2𝑡−𝑥 /𝑦+z
\(\dfrac{x}{y}=\dfrac{y}{z}=\dfrac{z}{t}=\dfrac{t}{x}=\dfrac{x+y+z+t}{y+z+t+x}=1\\ \Rightarrow\left\{{}\begin{matrix}x=y\\y=z\\z=t\\t=x\end{matrix}\right.\Rightarrow x=y=z=t\\ \Rightarrow M=\dfrac{2x-x}{x+x}+\dfrac{2x-x}{x+x}+\dfrac{2x-x}{x+x}+\dfrac{2x-x}{x+x}=\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{1}{2}=2\)
Đúng 1
Bình luận (0)
Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào biến:
c) (𝑥 − 5)(𝑥 + 8) − (𝑥 + 4)(𝑥 − 1); d) 𝑦^4 − (𝑦^2 − 1)(𝑦^2 + 1);
c: \(=x^2+3x-40-x^2-3x+4=-36\)
Đúng 1
Bình luận (1)
Câu 1: Trong khẳng định sau, khẳng định nào sai?A. 2023 ∈ NB. sqrt{2023}∈ RC. -2023 ∈ ZD. sqrt{2023} ∈ QCâu 2: Từ tỉ lệ thức dfrac{a}{b}dfrac{c}{d} ta không suy ra được tỉ lệ thức nào trong các tỉ lệ thức sau? (Với giả thiết các tỉ số đều có nghĩa)A. dfrac{a}{c}dfrac{b}{d}B. dfrac{d}{c}dfrac{b}{a}C. dfrac{a}{b-c}dfrac{c}{d-a}D. dfrac{a+c}{b+d}dfrac{a-c}{b-d}Câu 3: Trong các số sau: sqrt{dfrac{9}{49}};sqrt{49};sqrt{0,9};sqrt{0,03} số nào là số vô tỉ?
Đọc tiếp
Câu 1: Trong khẳng định sau, khẳng định nào sai?
A. 2023 ∈ N
B. \(\sqrt{2023}\)∈ R
C. -2023 ∈ Z
D. \(\sqrt{2023}\) ∈ Q
Câu 2: Từ tỉ lệ thức \(\dfrac{a}{b}=\dfrac{c}{d}\) ta không suy ra được tỉ lệ thức nào trong các tỉ lệ thức sau? (Với giả thiết các tỉ số đều có nghĩa)
A. \(\dfrac{a}{c}=\dfrac{b}{d}\)
B. \(\dfrac{d}{c}=\dfrac{b}{a}\)
C. \(\dfrac{a}{b-c}=\dfrac{c}{d-a}\)
D. \(\dfrac{a+c}{b+d}=\dfrac{a-c}{b-d}\)
Câu 3: Trong các số sau: \(\sqrt{\dfrac{9}{49}};\sqrt{49};\sqrt{0,9};\sqrt{0,03}\) số nào là số vô tỉ?
Câu 1: D
Câu 2: C
Câu 3:
\(\sqrt{\dfrac{9}{49}}=\sqrt{\left(\dfrac{3}{7}\right)^2}=\dfrac{3}{7}\) là số hữu tỉ
\(\sqrt{49}=7\) là số hữu tỉ
\(\sqrt{0,9}=\sqrt{\dfrac{9}{10}}=\dfrac{3}{\sqrt{10}}\) là số vô tỉ
\(\sqrt{0,03}\) là số vô tỉ
=>Trong các số này có hai số là số vô tỉ đó là \(\sqrt{0,9};\sqrt{0,03}\)
Đúng 1
Bình luận (0)
Câu 4: Cho đẳng thức: . Tỉ lệ thức được suy ra từ đẳng thức là:
Đọc tiếp
Câu 4: Cho đẳng thức: . Tỉ lệ thức được suy ra từ đẳng thức là:
. Tỉ lệ thức được suy ra từ đẳng thức là:
Câu 1: Từ tỉ lệ thức \(\frac{b}{a}=\frac{d}{c}\) với a,b,c,d\(\ne\) 0, ta suy ra các đẳng thức:
A, ab = cd B, ad = bc C, ac = bd D, a : d = b : c
Câu B bạn nhé! Tick ủng hộ mình nha!
Đúng 0
Bình luận (0)
a) Lập tất cả các tỉ lệ thức từ các đẳng thức sau:i) 14.15 10. 21 ii) AB.CD 2.3iii) AB.CD EF.GH iv) 4.AB 5.MN.b) Lập tất cả các tỉ lệ thức có thể từ tỉ lệ thức sau:
−
5
15
−
1
,
2
3
,
6
.c) Lập tất cả các tỉ lệ thức có được t...
Đọc tiếp
a) Lập tất cả các tỉ lệ thức từ các đẳng thức sau:
i) 14.15 = 10. 21 ii) AB.CD = 2.3
iii) AB.CD = EF.GH iv) 4.AB = 5.MN.
b) Lập tất cả các tỉ lệ thức có thể từ tỉ lệ thức sau: − 5 15 = − 1 , 2 3 , 6 .
c) Lập tất cả các tỉ lệ thức có được từ bôn số sau: 12; - 3; 40; -10.
7) a) Tìm giá trịnhỏnhất của biểu thức: 𝐴(𝑥−1)(𝑥−3)+11b) Tìm giá trịlớn nhất của biểu thức: 𝐵5−4𝑥2+4𝑥c) Cho 𝑥–𝑦2. Tìm giá trịlớn nhất của đa thức 𝐵𝑦2−3𝑥28) Tìm số𝑎đểđa thức 𝑥3−3𝑥2+5𝑥+𝑎chia hết cho đa thức 𝑥−2
Đọc tiếp
7) a) Tìm giá trịnhỏnhất của biểu thức: 𝐴=(𝑥−1)(𝑥−3)+11
b) Tìm giá trịlớn nhất của biểu thức: 𝐵=5−4𝑥2+4𝑥
c) Cho 𝑥–𝑦=2. Tìm giá trịlớn nhất của đa thức 𝐵=𝑦2−3𝑥2
8) Tìm số𝑎đểđa thức 𝑥3−3𝑥2+5𝑥+𝑎chia hết cho đa thức 𝑥−2
\(7,\\ a,A=x^2-4x+3+11=\left(x-2\right)^2+10\ge10\\ \text{Dấu }"="\Leftrightarrow x=2\\ b,B=-\left(4x^2-4x+1\right)+6=-\left(2x-1\right)^2+6\le6\\ \text{Dấu }"="\Leftrightarrow x=\dfrac{1}{2}\\ c,x-y=2\Leftrightarrow x=y+2\\ \Leftrightarrow B=y^2-3x^2=y^2-3\left(y+2\right)^2\\ \Leftrightarrow B=y^2-3y^2-12y-12=-4y^2-12y-12\\ \Leftrightarrow B=-\left(4y^2+12y+9\right)-3=-\left(2y+3\right)^2-3\le-3\\ \text{Dấu }"="\Leftrightarrow y=-\dfrac{3}{2}\Leftrightarrow x=\dfrac{1}{2}\)
\(8,\\ \Leftrightarrow x^3-3x^2+5x+a=\left(x-2\right)\cdot a\left(x\right)\)
Thay \(x=2\Leftrightarrow8-12+10+a=0\Leftrightarrow a=-6\)
Đúng 0
Bình luận (1)