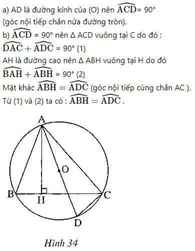
Cho tam giác ABC nội tiếp (O),đường cao AH.Vẽ đường kính AD của (O).Chứng minh rằng góc BAH = góc CAD.

Những câu hỏi liên quan
Cho tam giác ABC nội tiếp (O),đường cao AH.Vẽ đường kính AD của (O).Chứng minh rằng góc BAH = góc CAD.
Cho tam giác ABC nội tiếp (O),đường cao AH.Vẽ đường kính AD của (O).Chứng minh rằng góc BAH = góc CAD.
Giúp mình vớii :((
\(BAH=CAD=90\) độ (góc nội tiếp chắn nửa đường tròn)
Đúng 1
Bình luận (3)
Cho tam giác nhọn ABC nội tiếp trong đường tròn (O), AB < AC. Kẻ đường cao AH của tam giác. H thuộc BC và đường kính AD của đường tròn (O).
1. Chứng minh rằng tam giác BAH đồng dạng tam giác DAC.
2. Kẻ BK vuông góc AD, K thuộc AD. Chứng minh rằng tứ giác ABHK nội tiếp.
3. Chứng minh rằng đường thẳng HK vuông góc AC.
Cho tam giác ABC nội tiếp đường tròn (O) đường kính AD. Kẻ đường cao AH
a) Chứng minh tam giác BAH và tam giác CAD đồng dạng
b) Gọi I là điểm chính giữa cung BC (không chứa điểm A). Chứng minh AI là tia phân giác của góc HAD
cho tam giác ABC nhọn nội tiếp đường tròn (O) có đường cao AH . Chứng minh rằng góc BAH = góc OAC
cho tam giác nhọn ABC nôi tiếp đường tròn tâm O, các đường cao AM,BN,CP căt nhau tại H. a. cm tứ giác ANHP nội tiếp b. kẻ đường kính AD của đường tròn O. Cm góc BAM= góc CAD c. cm AD vuông góc NP d. Gọi R là bán kính đường tròn ngoại tiếp tứ giác BCNP . Cm BH.BN+CH.CP=4R^2 e. Gợi I là trung điểm B. CM AH=1OI
XIn các bạn giải giùm mình
Mình cần gắp lắm ạ
Đúng 0
Bình luận (0)
cho tam giác abc có ba góc nhọn nội tiếp ( O ).gọi H là giao điểm của ba đường cao AD,BE,CF của tam giác ABC.
a) chứng minh rằng AEHF là tứ giác nội tiếp
b) vẽ đường kính AK của ( O ). chứng minh AB.AC=AK.AD
Cho tam giác ABC có ba góc nhọn, AB < AC, nội tiếp đường tròn ( O, R). Vẽ đường kính AD của đường tròn ( O ), đường cao AH của tam giác ABC ( H thuộc BC ) và BE vuông góc với AD ( E thuộc AD ).
a) Chứng minh tứ giác AEHB nội tiếp
b) Chứng minh AH.DC = AC.BH
c) Gọi I là trung điểm của BC. Chứng minh rằng IH = IE
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O),đường cao AH.Kẻ đường kính AM.
a.Tính góc ACM.
b.Chứng minh góc BAH = góc OA
\(a,\widehat{ACM}=90^0\) (góc nt chắn nửa đg tròn)
\(b,\widehat{BAH}+\widehat{ABH}=90^0;\widehat{OAC}+\widehat{AMC}=90^0\left(\widehat{ACM}=90^0\right)\)
Mà \(\widehat{ABH}=\widehat{AMC}\left(=\dfrac{1}{2}sđ\stackrel\frown{AC}\right)\)
Do đó \(\widehat{BAH}=\widehat{OAC}\)
Đúng 0
Bình luận (0)