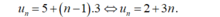Cho dãy số (un) biết u1 = 3; \(u_{n+1}=\sqrt{1+u_n^2}\) với \(n\ge1\). Tìm công thức của số hạng tổng quát un
Những câu hỏi liên quan
Cho dãy số (un) biết
u
1
2
u
2
2
u
n
u...
Đọc tiếp
Cho dãy số (un) biết u 1 = 2 u 2 = 2 u n = u n - 2 - 2 u n - 1 n ≥ 3 Số hạng thứ 4 của dãy số (un) bằng
A. 0
B. 21
C. -9
D. 34
Cho dãy số
u
n
, biết
u
1
-
1
,
u
n
+
1
u
n
+
3
v
ớ
i
n
≥...
Đọc tiếp
Cho dãy số u n , biết u 1 = - 1 , u n + 1 = u n + 3 v ớ i n ≥ 1 .
a. Viết năm số hạng đầu của dãy số;
b. Chứng minh bằng phương pháp quy nạp: u n = 3 n – 4
a. u1 = - 1, un + 1 = un + 3 với n > 1
u1 = - 1;
u2 = u1 + 3 = -1 + 3 = 2
u3 = u2 + 3 = 2 + 3 = 5
u4 = u3 + 3 = 5 + 3 = 8
u5 = u4 + 3 = 8 + 3 = 11
b. Chứng minh phương pháp quy nạp: un = 3n – 4 (1)
+ Khi n = 1 thì u1 = 3.1 - 4 = -1, vậy (1) đúng với n = 1.
+ Giả sử công thức (1) đúng với n = k > 1 tức là uk = 3k – 4.
+ Ta chứng minh (1) đúng với n= k+ 1 tức là chứng minh: uk+1 = 3(k+1) - 4
Thật vậy,ta có : uk + 1 = uk + 3 = 3k – 4 + 3 = 3(k + 1) – 4.
⇒ (1) đúng với n = k + 1
Vậy (1) đúng với ∀ n ∈ N*.
Đúng 0
Bình luận (0)
Cho dãy
u
n
biết
u
1
1
u
n
+
1...
Đọc tiếp
Cho dãy u n biết u 1 = 1 u n + 1 = u n + 1 2 n . Xác định số hạng tổng quát của dãy u n
A. 2 - 0 , 5 n - 1
B. 0 , 5 n - 1
C. 0 , 5 n
D. Tất cả sai
Cho dãy số
u
n
biết
u
1
1
u
n
+
1...
Đọc tiếp
Cho dãy số u n biết u 1 = 1 u n + 1 = 2 u n + 3 . Số hạng thứ 15 của dãy số là?
A. 65533
B. 65539
C. 65545
D. 65535
Đáp án A
Em cần tìm ra quy luật của dãy số và từ đó tính số hạng tổng quát
Em có:
Đúng 0
Bình luận (0)
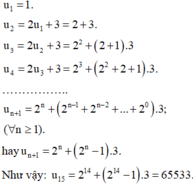
Cho cấp số nhân (un) biết u1 = 3/2 và q = 1/2. Số u1=3/512 là số hạng thứ mấy của dãy
\(u_n=u_1\cdot q^{n-1}\\ \Rightarrow\dfrac{3}{512}=\dfrac{3}{2}\cdot\left(\dfrac{1}{2}\right)^{n-1}\\ \Leftrightarrow\left(\dfrac{1}{2}\right)^{n-1}=\dfrac{1}{256}\\ \Leftrightarrow\left(\dfrac{1}{2}\right)^{n-1}=\dfrac{1}{2^8}\\ \Leftrightarrow n-1=8\\ \Leftrightarrow n=9\)
Vậy \(\dfrac{3}{512}\) là số hạng thứ 9 của dãy.
Đúng 1
Bình luận (0)
Cho dãy số
u
n
biết
u
1
2
u
n
+
1...
Đọc tiếp
Cho dãy số u n biết u 1 = 2 u n + 1 = 2 u n ∀ n ∈ N * . Tìm số hạng tổng quát của dãy số này?
A. u n = 2 n
B. u n = n n − 1
C. u n = 2
D. u n = 2 n + 1
Cho dãy số
u
n
là một cấp số cộng có
u
1
3
và công sai d4. Biết tổng n số hạng đầu của dãy số
u
n
là
S
n
253
. Tìm n? A. 10 B. 9 C. 12 D. 11
Đọc tiếp
Cho dãy số u n là một cấp số cộng có u 1 = 3 và công sai d=4. Biết tổng n số hạng đầu của dãy số u n là S n = 253 . Tìm n?
A. 10
B. 9
C. 12
D. 11
Cho dãy số (un)(��) biết : u1−1;un+1un+3�1−1;��+1��+3 với n≥1�≥1Viết năm số hạng đầu và tìm công thức tính số hạng tổng quát un theo n
Đọc tiếp
Cho dãy số biết :
với
Viết năm số hạng đầu và tìm công thức tính số hạng tổng quát un theo n
u1=-1
u2=-1+3=2
u3=2+3=5
u4=5+3=8
u5=8+3=11
Công thức tổng quát là: \(U_n=U_1+\left(n-1\right)\cdot\left(3\right)=-1+3n-3=3n-4\)
Đúng 1
Bình luận (0)
Cho dãy số
u
n
xác định bởi
u
1
5
và
u
n
+
1
3
+
u
n
. Số hạng tổng quát của dãy số này là: A.
u
n
8
+
n
B.
u
n...
Đọc tiếp
Cho dãy số u n xác định bởi u 1 = 5 và u n + 1 = 3 + u n . Số hạng tổng quát của dãy số này là:
A. u n = 8 + n
B. u n = 2 + 3 n
C. u n = 5 + 3 n
D. u n = 5 . 3 n
Chọn B.
- Ta có, u 1 = 5 và u n + 1 = 3 + u n nên dãy số là cấp số cộng với công sai d = 3, số hạng đầu u 1 = 5 .
- Do đó số hạng tổng quát của dãy số này là:
Đúng 0
Bình luận (0)