Cho hàm số y=(m-2)x + 3 (1) Với giá trị nào của m thì đường thẳng đi qua A(2;3)

Những câu hỏi liên quan
Bài 8. Cho hàm số y = (m - 2)x + m + 1 (d)
1) Với giá trị nào của m thì hàm số đã cho là hàm số bậc nhất ?
2) Tìm giá trị của m để đường thẳng (d) đi qua gốc tạo độ
3) Tim giá trị của m để đường thẳng (d) đi qua điểm A(2; 3)
4) Tìm giá trị của m để đường thẳng (d) tạo với trục Ox một góc tù
5) Tim m để đường thẳng (d) song song với đường thẳng y 3x +2 (d1)
Cho hàm số (d): y = (m - 3)x + m + 1
a) Với giá trị nào của m thì hàm số (d) đồng biến, nghịch biến?
b) Tìm giá trị của m để đường thẳng (d) đi qua gốc tọa độ.
c) Xác định giá trị của m để đường thẳng (d) đi qua H(1; 2)
Cho hàm số bậc nhất y (2 - 5m)x + m - 3 có đồ thị là (d)a) với những giá trị nào của m thì đường thẳng d đi qua gốc tọa độ?b) với những giá trị nào của m thì đường thẳng d tạo với tia Ox một góc nhọn? Một góc tù?c) tìm giá trị của m để đường thẳng d cắt trục tung tại điểm có tung độ bằng dfrac{2}{3}d) tìm m để đường thẳng d cắt trục hoành tại điểm có hoành độ bằng dfrac{1}{2}
Đọc tiếp
Cho hàm số bậc nhất y = (2 - 5m)x + m - 3 có đồ thị là (d)
a) với những giá trị nào của m thì đường thẳng d đi qua gốc tọa độ?
b) với những giá trị nào của m thì đường thẳng d tạo với tia Ox một góc nhọn? Một góc tù?
c) tìm giá trị của m để đường thẳng d cắt trục tung tại điểm có tung độ bằng \(\dfrac{2}{3}\)
d) tìm m để đường thẳng d cắt trục hoành tại điểm có hoành độ bằng \(\dfrac{1}{2}\)
a: Thay x=0 và y=0 vào (d), ta được:
\(0\left(2-5m\right)+m-3=0\)
=>m-3=0
=>m=3
b: Để (d) tạo với trục Ox một góc nhọn thì 2-5m>0
=>5m<2
=>\(m< \dfrac{2}{5}\)
Để (d) tạo với trục Ox một góc tù thì 2-5m<0
=>5m>2
=>\(m>\dfrac{2}{5}\)
c: Thay x=0 và \(y=\dfrac{2}{3}\) vào (d), ta được:
\(0\left(2-5m\right)+m-3=\dfrac{2}{3}\)
=>\(m-3=\dfrac{2}{3}\)
=>\(m=\dfrac{2}{3}+3=\dfrac{11}{3}\)
d: thay \(x=\dfrac{1}{2};y=0\) vào (d), ta được:
\(\dfrac{1}{2}\left(2-5m\right)+m-3=\dfrac{2}{3}\)
=>\(1-\dfrac{5}{2}m+m-3=\dfrac{2}{3}\)
=>\(-\dfrac{3}{2}m-2=\dfrac{2}{3}\)
=>\(-\dfrac{3}{2}m=2+\dfrac{2}{3}=\dfrac{8}{3}\)
=>\(m=-\dfrac{8}{3}:\dfrac{3}{2}=-\dfrac{16}{9}\)
Đúng 1
Bình luận (0)
Cho 2 hàm số bậc nhất y = (3m - 1)x + 2 và y = (m + 3)x +1
a) Với giá trị nào của m thì đồ thị của 2 hàm số là 2 đường thẳng song song với nhau?
b) Với giá trị nào của m thì đò thị của 2 hàm số là 2 đường thẳng cắt nhau?
\(a,\Leftrightarrow3m-1=m+3\Leftrightarrow2m=4\Leftrightarrow m=2\\ b,\Leftrightarrow3m-1\ne m+3\Leftrightarrow m\ne2\)
Đúng 4
Bình luận (0)
Câu 3: cho hàm số y = ( m - 3 ) x a, Với giá trị nào của m thì hàm số đồng biến? Nghịch biến? b, Với giá trị nào của m thì hàm số đi qua A (1,2) C, Với giá trị nào của m thì hàm số đi qua B (1,2) D, Vẽ đô thị của 2 hàm số ứng với m vừa tìm đc ở câu a,b
a: Để hàm số đồng biến trên R thì m-3>0
=>m>3
Để hàm số nghịch biến trên R thì m-3<0
=>m<3
b: Thay x=1 và y=2 vào y=(m-3)x, ta được:
\(1\left(m-3\right)=2\)
=>m-3=2
=>m=5
c: Thay x=1 và y=2 vào y=(m-3)x, ta được:
m-3=2
=>m=5
d: Khi m=5 thì y=(5-3)x=2x
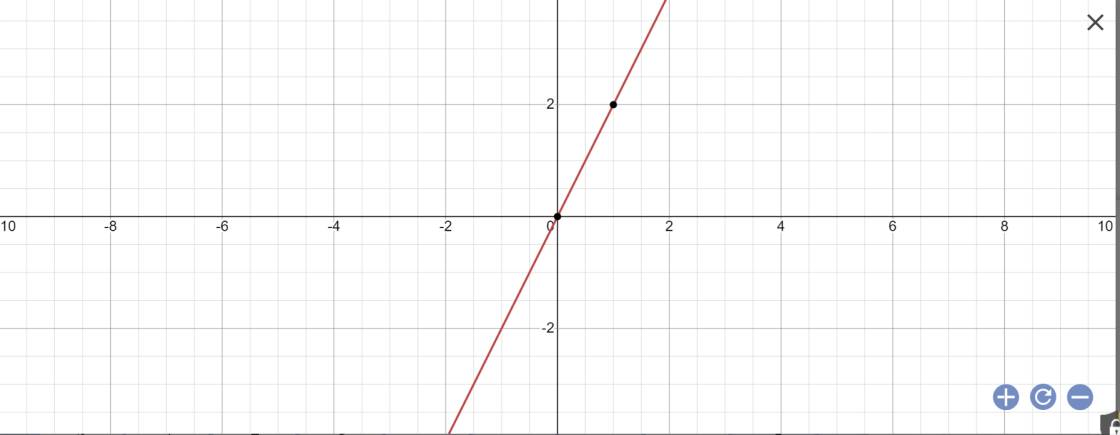
Đúng 2
Bình luận (0)
Cho hai hàm số y = (m - 1)x + 3 và y = (3 - m)x + 1, Với giá trị nào của m thì đồ thị của hai hàm só là hai đường thẳng song song với nhaub, Với giá trị nào của m thì đồ thị của 2 hàm số là hai đường thẳng cắt nhau
a: Để hai đường thẳng song song thì m-1=3-m
=>2m=4
hay m=2
Đúng 0
Bình luận (0)
\(\text{//}\Leftrightarrow m-1=3-m\Leftrightarrow m=2\\ \cap\Leftrightarrow m-1\ne3-m\Leftrightarrow m\ne2\)
Đúng 0
Bình luận (0)
Cho hàm số bậc nhất y = (m - 2)x + m + 1 với m là tham số có đồ thị là đường thẳng (d).
1. Tìm m để (d) đi qua điểm A(1; -1). Vẽ (d) với m vừa tìm được.
2. Với giá trị nào của m thì (d) và đường thẳng (d’) : y = 1 - 3x song song với nhau?
3. Tìm m để khoảng cách từ gốc toạ độ O đến (d) = 1
1: Thay x=1 và y=1 vào (d), ta được:
2m-1=-1
hay m=0
Đúng 0
Bình luận (0)
Cho đường thẳng y=(m-2)x + m (d)
a) Với giá trị nào của m thì đường thẳng (d) đi qua gốc tọa độ?
b) Với giá trị nào của m thì đường thẳng (d) đi qua điểm A(2;5)
c) Với giá trị nào của m thì đường thẳng (d) cắt đường thẳng y = 3x - 2
cho 2 hàm số y=\(\dfrac{m-1}{m+1}\)x +m+2 (1)
a, với giá trị nào thì hàm số (1) là hàm số bậc nhất
b, với giá trị nào thì hàm số (1) là hàm số đồng biến
c, với giá trị nào của m thì đồ thị hàm số (1) đi qua điểm A(1;2)
\(a,\Leftrightarrow\dfrac{m-1}{m+1}\ne0\Leftrightarrow m\ne\pm1\\ b,\Leftrightarrow\dfrac{m-1}{m+1}>0\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -1\end{matrix}\right.\\ c,\Leftrightarrow\dfrac{m-1}{m+1}+m+2=2\\ \Leftrightarrow\dfrac{m-1+m^2+m}{m+1}=0\\ \Leftrightarrow m^2+2m-1=0\\ \Leftrightarrow\left[{}\begin{matrix}m=-1+\sqrt{2}\\m=-1-\sqrt{2}\end{matrix}\right.\)
Đúng 1
Bình luận (0)














