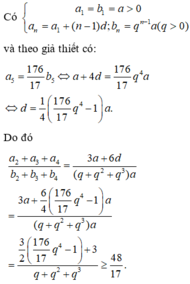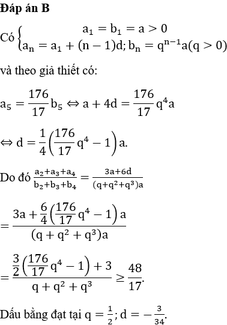cho a,b là các số dương thỏa mãn :a3+b3= a5+b5 cmr : a2+b2 \(\le\)1+a.b

Những câu hỏi liên quan
cho a,b là 2 số thực phân biệt thỏa mãn a2-3a=b2-3b=1. Tính giá trị của:
a+b ; a2+b2 ; a3+b3 ; a4+b4 ; a5+b5 ; a6+b6
cho 5 số nguyên a1,a2,a3,a4,a5. Gọi b1,b2,b3,b4,b5 là hoán vị của 5 số đã cho.
CMR: (a1-b1).(a2-b2).(a3-b3).(a5-b5) chia hết cho 2
Bài này lớp 6 mà bạn
Đặt c1=a1-b1, ... , c5=a5-b5.
Có c1+ c2 + ...+ c5
= (a1-b1)+(a2-b2)+...+(a5-b5)
= (a1+a2+...+a5)-(b1+b2+...+b5)
=0 (vì b1, b2, b3, b4, b5 là hoán vị của a1, a2, a3, a4, a5)
=> Trong 5 số c1,...,c5 có một số chẵn vì từ c1 đến c5 có 5 số
=> Trong các số a1-b1,...,a2-b2 có một số chẵn
Vậy ... (đpcm)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho các số thực dương
a
1
,
a
2
,
a
3
,
a
4
,
a
5
theo thứ tự lập thành cấp số cộng và các số thực dương
b
1
,
b
2
,
b
3
,...
Đọc tiếp
Cho các số thực dương a 1 , a 2 , a 3 , a 4 , a 5 theo thứ tự lập thành cấp số cộng và các số thực dương b 1 , b 2 , b 3 , b 4 , b 5 theo thứ tự lập thành cấp số nhân. Biết rằng a 1 = b 1 và a 5 = 176 17 b 5 Giá trị nhỏ nhất của biểu thức a 2 + a 3 + a 4 b 2 + b 3 + b 4 bằng
A. 16 17
B. 48 17
C. 32 17
D. 24 17
Cho các số thực dương
a
1
,
a
2
,
a
3
,
a
4
,
a
5
theo thứ tự lập thành cấp số cộng và các số thực dương
b
1
,
b
2
,
b
3
,
b
4...
Đọc tiếp
Cho các số thực dương a 1 , a 2 , a 3 , a 4 , a 5 theo thứ tự lập thành cấp số cộng và các số thực dương b 1 , b 2 , b 3 , b 4 , b 5 theo thứ tự lập thành cấp số nhân. Biết rằng a 1 = b 1 và a 5 = 176 17 b 5 . Giá trị nhỏ nhất của biểu thức a 2 + a 3 + a 4 b 2 + b 3 + b 4 bằng
A. 16 17
B. 48 17
C. 32 17
D. 24 17
Cho 5 số nguyên a1, a2, a3, a4 ,a5. Gọi b1, b2, b3, b4, b5 là hoán vị của 5 số đã cho
Chứng minh rằng tích (a1-b1)(a2-b2)(a3-b3)(a4-b4)(a5-b5)
Các bạn giúp mình với mình cảm ơn
Cho 5 số nguyên a1,a2,a3,a4,a5 . Gọi b1,b2,b3,b4,b5 là hoán vị của 5 đã số đã cho . Chứng minh rằng tích (a1 - b1 ).(a2 -b2).(a3 - b3).(a4 - a4).(a5 - b5) chia hết cho 2
Các bạn giúp mik thì mik cảm ơn rất nhìu <3
cho các số dương a,b thỏa mãn : a2+b2 = a3+b3 =a4+b4. tính a+b
\(a^2+b^2=a^3+b^3=a^4+b^4\)
\(\Rightarrow\left(a^3+b^3\right)^2=\left(a^2+b^2\right)\left(a^4+b^4\right)\)
\(\Rightarrow a^6+b^6+2a^3b^3=a^6+b^6+a^2b^4+a^4b^2\)
\(\Rightarrow2a^3b^3=a^2b^2\left(a^2+b^2\right)\)
\(\Rightarrow2ab=a^2+b^2\)
\(\Rightarrow\left(a-b\right)^2=0\)
\(\Rightarrow a=b\)
Thế vào \(a^2+b^2=a^3+b^3\)
\(\Rightarrow a^2+a^2=a^3+a^3\Rightarrow2a^3=2a^2\Rightarrow a=b=1\)
\(\Rightarrow a+b=2\)
Đúng 0
Bình luận (0)
cho a,b,c là 3 số dương thỏa mãn: a+b+c=2019. Tìm GTNN : a3/a2+b2+ab + b3/b2+c2+bc + c3/c2+a2+ca
Đặt \(P=\dfrac{a^3}{a^2+b^2+ab}+\dfrac{b^3}{b^2+c^2+bc}+\dfrac{c^3}{c^2+a^2+ca}\)
Ta có: \(\dfrac{a^3}{a^2+b^2+ab}=a-\dfrac{ab\left(a+b\right)}{a^2+b^2+ab}\ge a-\dfrac{ab\left(a+b\right)}{3\sqrt[3]{a^3b^3}}=a-\dfrac{a+b}{3}=\dfrac{2a-b}{3}\)
Tương tự: \(\dfrac{b^3}{b^2+c^2+bc}\ge\dfrac{2b-c}{3}\) ; \(\dfrac{c^3}{c^2+a^2+ca}\ge\dfrac{2c-a}{3}\)
Cộng vế:
\(P\ge\dfrac{a+b+c}{3}=673\)
Dấu "=" xảy ra khi \(a=b=c=673\)
Đúng 0
Bình luận (0)
cho A1,A2,A3,...,An là các số nguyênva B1,B2.B3,...,Bn là các hoán vị .CMR: (A1-B1)*(A2-B2)*(A3-B3)*...*(An-An) là số chẵn nếu A1,A2,A3,...,An la so le
Cho a + b + c = 0. Chứng minh : (a2 + b2 + c2 )/2 * (a3 + b3 + c3 )/3 = (a5 + b5 + c5 )/5