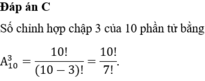Số chỉnh hợp chập 3 của 8 phần tử là?
Những câu hỏi liên quan
Cho tập hợp A = {a, b, c, d, e}.
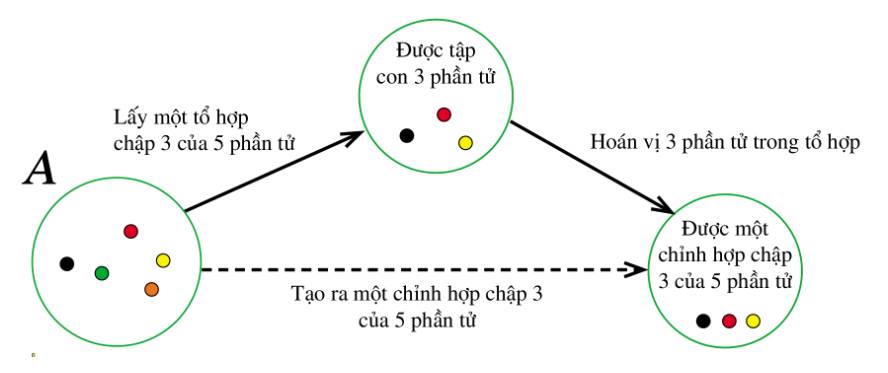
a) Nêu cách lấy ra một tổ hợp chập 3 của 5 phần tử trong A.
b) Nêu cách lấy ra một chỉnh hợp chập 3 của 5 phần tử trong A.
c) So sánh cách lấy ra một chỉnh hợp chập 3 của 5 phần tử trong A với cách lấy ra một tổ hợp chập 3 của 5 phần tử trong A.
a) Cách lấy ra một tổ hợp chập 3 của 5 phần tử trong A là: Chọn bất kỳ 3 trong 5 phần tử thuộc A ví dụ như \(\left\{ {a;b;c} \right\}\)
b) Cách lấy ra một chỉnh hợp chập 3 của 5 phần tử trong A là: Chọn bất kỳ 3 trong 5 phần tử thuộc A rồi sắp xếp theo một thứ tự nào ví dụ như ta chọn 3 phần tử a,b,c rồi sắp xếp theo thứ tự ngược của bảng chữ cái \(\left\{ {c;b;a} \right\}\)
c) So sánh: Mỗi tổ hợp chập 3 của 5 phần tử sinh ra 3! chỉnh hợp chập 3 của 5 phần tử vì có 3! hoán vị của 3 phần tử. Vì thế, số chỉnh hợp chập 3 của 5 phần tử nhiều gấp 3! lần số tổ hợp chập 3 của 5 phần tử.
Đúng 0
Bình luận (0)
Số chỉnh hợp chập 3 của 10 phần tử
A . P 3
B . C 10 3
C . P 10
D . A 10 3
Số chỉnh hợp chập 4 của 7 phần tử là:
A. 720
B. 35
C. 840
D. 24
Số chỉnh hợp chập 3 của 10 phần tử bằng A.
C
10
3
. B.
10
!
3
!
C.
10
!
7
!
D.
10...
Đọc tiếp
Số chỉnh hợp chập 3 của 10 phần tử bằng
A. C 10 3 .
B. 10 ! 3 !
C. 10 ! 7 !
D. 10 ! - 3 !
Đáp án C
Số chỉnh hợp chập 3 của 10 phần tử bằng
Đúng 0
Bình luận (0)
Số chỉnh hợp chập 3 của 10 phần tử bằng
A. C 10 3
B. 10 ! 3 !
C. 10 ! 7 !
D. 10! - 3!
Số chỉnh hợp chập 3 của 10 phần tử bằng A.
C
10
3
B.
10
!
3
!
C.
10
!
7
!
D.
10
!
-
3
!
Đọc tiếp
Số chỉnh hợp chập 3 của 10 phần tử bằng
A. C 10 3
B. 10 ! 3 !
C. 10 ! 7 !
D. 10 ! - 3 !
Số chỉnh hợp chập 6 của một tập hợp có 9 phần tử là:
A. 9!/(3!.6!).
B. 6!/3!.
C. 9!/6!.
D. 9!/3!.
Số chỉnh hợp chập 6 của một tập hợp có 9 phần tử là: A.
9
!
3
!
.
6
!
. B.
6
!
3
!
.
C. ...
Đọc tiếp
Số chỉnh hợp chập 6 của một tập hợp có 9 phần tử là:
A. 9 ! 3 ! . 6 ! .
B. 6 ! 3 ! .
C. 9 ! 6 ! .
D. 9 ! 3 ! .
Viết công thức tính số chỉnh hợp chập k của n phần tử, công thức tính số tổ hợp chập k của n phần tử. Cho ví dụ.
+ Số chỉnh hợp chập k của n phần tử:
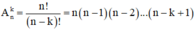
+ Số tổ hợp chập k của n phần tử:
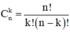
+ Ví dụ:
- Số chỉnh hợp chập 3 của 5: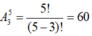 
- Số tổ hợp chập 3 của 5: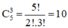 
- Chọn ngẫu nhiên 5 bông hoa trong số 8 bông hoa khác nhau để cắm vào 5 lọ khác nhau:
⇒ Có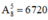 
cách chọn.
- Chọn ngẫu nhiên 5 bông hoa trong số 8 bông hoa khác nhau
⇒ Có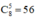 
cách chọn.
Đúng 0
Bình luận (0)