viết công thức tính tổng 12+22+.......+n2 (n(n+1)(2n+10/6
giup tui voi
Những câu hỏi liên quan
Câu 1: Viết chương trình tính tổng dãy số sau: S=12+22+...+n2.
Câu 2: Viết chương trình tính tổng nghịch đảo N số nguyên đầu tiên.
Câu 1:
var i,n:integer;
s:longint;
begin
write('Nhap n = ');readln(n);
for i:=1 to n do
s:=s+(i*10+2);
write('S = ',s);
readln;
end.
Câu 2:
var i,n:integer;
s:real;
begin
write('Nhap n = ');readln(n);
for i:=1 to n do s:=s+1/n;
write('tong la ',s:10:2);
readln;
end.
Đúng 2
Bình luận (0)
Với n là số tự nhiên, chứng minh:
n
+
1
-
n
2
2
n
+
1...
Đọc tiếp
Với n là số tự nhiên, chứng minh:
n + 1 - n 2 = 2 n + 1 2 - 2 n + 1 2 - 1
Viết đẳng thức trên khi n bằng 1, 2, 3, 4
Ta có:
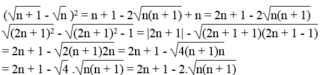
Vế trái bằng vế phải nên đẳng thức được chứng minh.
* Với n = 1, ta có: 2 - 1 2 = 9 - 8
* Với n = 2, ta có: 3 - 2 2 = 25 - 24
* Với n = 3, ta có: 4 - 3 2 = 49 - 48
* Với n = 4, ta có: 5 - 4 2 = 81 - 80
Đúng 0
Bình luận (0)
Xác định Input, Output và viết thuật toán tính tổng S = 1 2 + 2 2 + 3 2 + . . . . + N 2 (với N nhập từ bàn phím, N là số nguyên dương).
- Xác định bài toán (0,5đ)
Input: Nhập N và dãy a 1 , a 2 , . . . , a n
Output: Đưa ra kết quả tổng S
- Thuật toán (1,75đ):
Bước 1: Nhập N và a 1 , a 2 , . . . , a n
Bước 2: S ← 0; i ← 1
Bước 3: Nếu i >Nthì đưa ra S rồi kết thúc
Bước 4: Nếu ai⟨0 thì S ←S+ a i 2
Bước 5: i ← i + 1 và quay lại Bước 3
Đúng 0
Bình luận (0)
Viết chương trình tính tổng S=12+22+32+…+n2 Với n là số nguyên dương được nhập vào từ bàn phím
#include <bits/stdc++.h>
using namespace std;
long long n,i,s;
int main()
{
cin>>n;
s=0;
for (i=1; i<=n; i++) s=s+i*i;
cout<<s;
return 0;
}
Đúng 0
Bình luận (0)
Var s,i,n:longint;
Begin
Write('Nhap so luong so n = ');readln(n);
For i:=1 to n do
s:=s+i*i;
Write('Tong la ',s);
Readln;
End.
Đúng 0
Bình luận (0)
các bn giải chi tiết giúp nha .Viết công thức để tính tổng S= 1.2.3 +2.3.5 +...+n(n+1)(2n+1)
SOS
bài 1: chứng minh
Sn = 12 + 22 + 32 + ... + n2 = n.(n + 1).(2n+1)/1
bài 2: tìm x biết
a) (x+1) + (x+2) + (x+3) + ... +(x+10) = 5070
b) 1 + 2 + 3 + ... + x = 820
❤mong mn giúp mình ạ ❤
Bài 1 :
A = 12 + 22 + 32 +....+n2
A = 12 + 2.(1+1) + 3.(2 +1) + 4.( 3 +1) +.....+n(n-1 + 1)
A = 1 + 1.2 + 2 + 2.3 + 3 + 3.4 + 4 +.....+ n.(n-1) + n
A = ( 1 + 2 + 3 + 4 +....+n) + ( 1.2 + 2.3 + 3.4 +....+(n-1).n
A = (n+1).{(n-1):n+1)/2 +1/3.[1.2.3 +2.3.3 +.....+(n-1)n.3]
A = (n+1).n/2+1/3.[1.2.3 +2.3.(4-1)+ ...+(n-1).n [(n+1) - (n -2)]
A = (n+1)n/2+1/3.( 1.2.3 + 2.3.4 -1.2.3 +..+ (n-1)n(n+1)- (n-2)(n-1)n)
A =(n+1)n/2 + 1/3.(n-1)n(n+1)
A = n(n+1)[1/2 + 1/3 .(n-1)]
A = n.(n+1) \(\dfrac{3+2n-2}{6}\)
A= n.(n+1)(2n+1)/6
Bài 2 :
a, (x+1) +(x+2) + (x+3)+...+(x+10) = 5070
(x+10 +x+1).{( x+10 - x -1): 1 +1):2 = 5070
(2x + 11)10 : 2 = 5070
( 2x + 11)5 = 5070
2x+ 11 = 5070:5
2x = 1014 - 11
2x = 1003
x = 1003 :2
x = 501,5
b, 1 + 2 + 3 +...+x = 820
( x + 1)[ (x-1):1 +1] : 2 = 820
(x +1).x = 820 x 2
(x +1).x = 1640
(x +1) .x = 40 x 41
x = 40
Đúng 1
Bình luận (0)
Câu 4: Cho S = 12 + 22 + 32 + … + n2, với n là một số tự nhiên nhập từ bàn phím. Hãy viết chương trình sử dụng lệnh lặp While…do để tính tổng trên?
uses crt;
var i,n,s:integer;
begin
clrscr;
readln(n);
s:=0;
i:=0;
while i<=n do
begin
i:=i+1;
s:=s+i*i;
end;
writeln(s);
readln;
end.
Đúng 0
Bình luận (0)
1. Viết công thức để tính tổng S1.2.3+2.3.5+...+n.(n+1).(2n+1)2. Số nào lớn hơn: A(102010+1):(102011+1) hay B(102011+1):(102012+1)3. Cho 102+112+122 132+142. Hỏi ngoài 5 số trên còn có những bộ 5 số nào có tính chất như vậy không?4. Tìm a,b,c thỏa mãn đẳng thức: a2-2a+b2+4b+4c2-4c+60
Đọc tiếp
1. Viết công thức để tính tổng S=1.2.3+2.3.5+...+n.(n+1).(2n+1)
2. Số nào lớn hơn: A=(102010+1):(102011+1) hay B=(102011+1):(102012+1)
3. Cho 102+112+122 = 132+142. Hỏi ngoài 5 số trên còn có những bộ 5 số nào có tính chất như vậy không?
4. Tìm a,b,c thỏa mãn đẳng thức: a2-2a+b2+4b+4c2-4c+6=0
Bài 4:
Ta có:
\(a^2-2a+b^2+4b+4c^2-4c+6=0\)
\(\Leftrightarrow a^2-2a+1+b^2+4b+4+4c^2-4c+1\)
\(\Leftrightarrow\left(a^2-2b+1\right)+\left(b^2+4b+4\right)+\left(4c^2-4c+1\right)\)
\(\Leftrightarrow\left(a-1\right)^2+\left(b+2\right)^2+\left(2c-1\right)^2\)
Mà \(\hept{\begin{cases}\left(a-1\right)^2\ge0\\\left(b+2\right)^2\ge0\\\left(2c-1\right)^2\ge0\end{cases}}\)
\(\Rightarrow\left(a-1\right)^2+\left(b+2\right)^2+\left(2c-1\right)^2\ge0\)
Dấu "=" xảy ra khi \(\hept{\begin{cases}\left(a-1\right)^2=0\\\left(b+2\right)^2=0\\\left(2c-1\right)^2=0\end{cases}\Leftrightarrow\hept{\begin{cases}a=1\\b=-2\\c=\frac{1}{2}\end{cases}}}\)
Vậy \(\left(a,b,c\right)=\left(1;-2;\frac{1}{2}\right)\)
Đúng 0
Bình luận (0)
bài này mình biết làm r nè, mấy bài khác cơ =))
Đúng 0
Bình luận (0)
Tính B = 1.2.3 + 2.3.4 + ... + (n - 1)n(n + 1)
Tính C = 1.4 + 2.5 + 3.6 + ...+ n(n + 3)
Tính D = 12 + 22 + 32 + ... + n2
