Ta có:
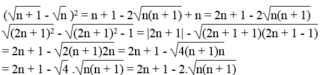
Vế trái bằng vế phải nên đẳng thức được chứng minh.
* Với n = 1, ta có: 2 - 1 2 = 9 - 8
* Với n = 2, ta có: 3 - 2 2 = 25 - 24
* Với n = 3, ta có: 4 - 3 2 = 49 - 48
* Với n = 4, ta có: 5 - 4 2 = 81 - 80
Ta có:
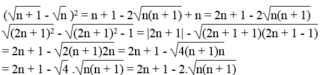
Vế trái bằng vế phải nên đẳng thức được chứng minh.
* Với n = 1, ta có: 2 - 1 2 = 9 - 8
* Với n = 2, ta có: 3 - 2 2 = 25 - 24
* Với n = 3, ta có: 4 - 3 2 = 49 - 48
* Với n = 4, ta có: 5 - 4 2 = 81 - 80
Với n là số tự nhiên, chứng minh đẳng thức:
n + 1 2 + n 2 = n + 1 2 - n 2
Viết đẳng thức trên khi n là 1, 2, 3, 4, 5, 6, 7
Các bạn ơi giải giúp mình với nha :
Rút gọn biểu thức:
\(\frac{1}{\sqrt{1}+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+...+\frac{1}{\sqrt{90}+\sqrt{100}}\)
Chứng minh đẳng thức :
\(\sqrt{n+1}-\sqrt{n}=\frac{1}{\sqrt{n+1}+\sqrt{n}}\)với n là số tự nhiên
Chứng minh các đại thức :
\(\left(\frac{6+4\sqrt{2}}{\sqrt{2}+\sqrt{6+4\sqrt{2}}}+\frac{6-4\sqrt{2}}{\sqrt{2}-\sqrt{6-4\sqrt{2}}}\right)^2=\sqrt{8}\)
Giúp mình với nhé!
Chứng minh đẳng thức: n + 1 - n = 1 n + 1 + n với n là số tự nhiên
chứng minh rằng với số tự nhiên n,n lớn hơn 4 ta có:
\(\dfrac{1}{2\sqrt{1}+1\sqrt{2}}+\dfrac{1}{3\sqrt{2}+2\sqrt{3}}+\dfrac{1}{4\sqrt{3}+3\sqrt{4}}+...+\dfrac{1}{\left(n+1\right)\sqrt{n}+n\sqrt{n+1}}< 1\)
Chứng minh bất đẳng thức
Với n thuộc N, chứng minh \(\sqrt{n+1}-\sqrt{n}>\frac{1}{2\sqrt{n+1}}\)
Sử dụng kết quả trên, chứng minh: \(1+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+...+\frac{1}{\sqrt{2012}}< 2.\sqrt{2012}\)
Chứng minh \(\frac{1}{2}.\frac{3}{4}.\frac{5}{6}.....\frac{2n-1}{2n}< \frac{1}{\sqrt{2n+1}}\)với n thuộc N*
Chứng minh với mọi số tự nhiên n>1 thì giá trị biểu thức \(E=\frac{3n^2}{2n^2+n-1}+\frac{1}{n+1}\)không thể là số tự nhiên
Với mọi n là số tự nhiên khác 0, chứng minh biểu thức
\(A_n=n+\left[\sqrt[3]{n-\frac{1}{27}}+\frac{1}{3}\right]^2\)không viết được dưới dạng lập phương của một số nguyên dương
chứng minh rằng với mọi số tự nhiên n≥1 thì (n+2)(n+1)(n+8) không thể là lập phương của một số tự nhiên.