Chứng minh rằng: a2 +b2 +c2 >=ab+ac+bc với mọi a. b. c

Những câu hỏi liên quan
Chứng minh rằng nếu a2+b2+c2-ab-bc-ac=0 thì a=b=c
Ta có :
\(\left(a-b-c\right)^2=a^2+b^2+c^2-2ab-2bc-2ac\)
mà theo đề bài \(a^2+b^2+c^2-ab-bc-ac=0\)
\(\Rightarrow\left(a-b-c\right)^2=-ab-bc-ac=0\)
\(\Rightarrow\left(a-b-c\right)^2=-\left(ab+bc+ac\right)=0\)
mà \(-\left(ab+bc+ac\right)\le0\)
\(\Rightarrow a=b=c=0\)
\(\Rightarrow dpcm\)
Đúng 4
Bình luận (0)
Cho a,b,c không âm. Chứng minh rằng :
a) a2 + b2 + c2 + 2abc + 2 > hoặc=ab +bc +ca +a+b+c
b)a2 + b2 +c2 +abc +4 > hoặc = 2(ab+bc+ca)
c) 3(a2 + b2 + c2) + abc +4 > hoặc =4 (ab+bc+ca)
d) 3(a2 + b2 + c2) + abc +80 > 4(ab+bc+ca) + 8(a+b+c)
Ngu kkkkkkkkkkkkkkkkkkkkkkkkkkkkkk
chứng minh: a2+b2+c2\(\ge\)ab+bc+ca với mọi a,b,c
=>2a^2+2b^2+2c^2-2ab-2bc-2ac>=0
=>(a-b)^2+(b-c)^2+(a-c)^2>=0(luôn đúng)
Đúng 1
Bình luận (0)
Xét hiệu a^2+b^2+c^2-ab-ac-bc=1/2.2(a^2+b^2+c^2-ab-ac-bc)
=1/2(2a^2+2b^2+2c^2-2ab-2ac-2bc)
=1/2[(a^2-2ab+b^2)+(a^2-2ac+c^2)+(b^2-2bc+c^2)]
=1/2.[(a-b)^2+(a-c)^2+(b-c)^2]
vì (a-b)^2+(a-c)^2+(b-c)^2>=0
nên 1/2.[(a-b)^2+(a-c)^2+(b-c)^2]>=0
hay a^2+b^2+c^2-ab-ac-bc >=0<=> a^2+b^2+c^2>=ab+ac+bc
Đúng 0
Bình luận (0)
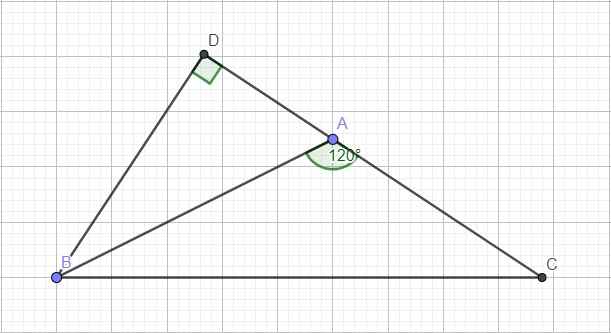
Cho tam giác ABC có góc A = 120 độ, BC = a, AC = b, AB = c. Chứng minh rằng a2 = b2 + c2 + bc ?
Kẻ đường cao BD ứng với AC. Do góc A tù \(\Rightarrow\) D nằm ngoài đoạn thẳng AC hay \(CD=AD+AC\) và \(\widehat{DAB}=180^0-120^0=60^0\)
Áp dụng định lý Pitago:
\(AB^2=BD^2+AD^2\) \(\Rightarrow BD^2=AB^2-AD^2\)
Trong tam giác vuông ABD:
\(cos\widehat{BAD}=\dfrac{AD}{AB}\Rightarrow\dfrac{AD}{AB}=cos60^0=\dfrac{1}{2}\Rightarrow AD=\dfrac{1}{2}AB\)
\(\Rightarrow BD^2=AB^2-\left(\dfrac{1}{2}AB^2\right)=\dfrac{3}{4}AB^2\)
Pitago tam giác BCD:
\(BC^2=BD^2+CD^2=\dfrac{3}{4}AB^2+\left(AD+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\left(\dfrac{1}{2}AB+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\dfrac{1}{4}AB^2+AB.AC+AC^2\)
\(=AB^2+AB.AC+AC^2\)
Hay \(a^2=b^2+c^2+bc\)
Đúng 3
Bình luận (0)
Bài 2: (2,0 điểm)
a) Giải bất phương trình sau: 4x – 2 > 5x + 1
b) Chứng minh rằng a2 + b2 + c2 > ab + bc + ca với mọi số thực a,b,c
a) `4x-2>5x+1`
`<=>-x>3`
`<=>x<-3`
b) Theo BĐT Cauchy:
`a^2+b^2 >= 2ab`
Tương tự:
`b^2+c^2>=2bc`
`c^2+a^2>=2ca`
Cộng vế với vế: `2(a^2+b^2+c^2) >= 2(ab+bc+ca)`
`<=>a^2+b^2+c^2 >= ab+bc+ca` (ĐPCM)
Đúng 2
Bình luận (0)
a, \(4x-2>5x+1\Leftrightarrow-x>3\Leftrightarrow x< -3\)
b, Ta có : \(a^2+b^2+c^2\ge ab+bc+ca\)
\(2a^2+2b^2+2c^2\ge2ab+2bc+2ca\)
\(\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ac+a^2\right)\ge0\)
\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\)* luôn đúng *
Đúng 2
Bình luận (0)
Cho a2+b2+c2=ab+bc+ca. Chứng minh rằng a=b=c
Ta có
$$a^2+b^2+c^2-ab-bc-ca=0,$$
hay $$\dfrac{1}{2}\left[(a-b)^2+(b-c)^2 +(c-a)^2\right[ = 0.$$
Mà vế trái luôn không âm \(\forall a,b,c \in \mathbb{R}\), đẳng thức xảy ra khi $a=b=c.$
Vậy ta có điều cần chứng minh.
Đúng 2
Bình luận (0)
Ta có: \(a^2+b^2+c^2=ab+bc+ca\)
\(\Leftrightarrow2a^2+2b^2+2c^2-2ab-2bc-2ac=0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
\(\Leftrightarrow a=b=c\)
Đúng 1
Bình luận (0)
Cho a, b,c là độ dài ba cạnh tam giác. Chứng minh rằng: a/(a2 + bc) + 1/(b2+ ac) + s/(c2+ab) <= (a+b+c)/2abc
chứng minh rằng
nếu a2 + b2 + c2 = ab +ac + bc thì a = b= c
giúp e với ạ
chứng minh rằng
nếu a2 + b2 + c2 = ab +ac + bc thì a = b= c
Giải
Ta có: a^2 + b^2 + c^2 = ab + bc + ca
<=> 2.a^2 + 2.b^2 + 2.c^2 = 2.ab + 2.bc + 2.ca
<=> ( a^2 - 2ab + b^2 ) + ( b^2 - 2bc +c^2 ) + ( c^2 - 2ac + a^2 ) =0
<=> (a-b)^2 + (b-c)^2 + (c -a)^2 =0 (1)
Vì (a-b)^2 ; (b-c)^2 ; (c -a)^2 ≧ 0 với mọi a,b,c.
=> (a-b)^2 + (b-c)^2 + (c -a)^2 ≧ 0 (2)
Từ (1) và (2) khẳng định dấu "=" khi:
a - b = 0; b - c = 0 ; c - a = 0 => a=b=c
Vậy a=b=c.
Đúng 0
Bình luận (0)
\(a^2+b^2+c^2=ab+ac+bc\Leftrightarrow a^2+b^2+c^2-ab-ac-bc=0\)
\(\Leftrightarrow2a^2+2b^2+2c^2-2ab-2ac-2bc=0\Leftrightarrow\left(a-b\right)^2+\left(a-c\right)^2+\left(b-c\right)^2=0\)
\(\left\{{}\begin{matrix}a-b=0\\a-c=0\\b-c=0\end{matrix}\right.\)\(\Leftrightarrow a=b=c\)
Đúng 0
Bình luận (0)
Ta có: a^2 + b^2 + c^2 = ab + bc + ca
<=> 2.a^2 + 2.b^2 + 2.c^2 = 2.ab + 2.bc + 2.ca
<=> ( a^2 - 2ab + b^2 ) + ( b^2 - 2bc +c^2 ) + ( c^2 - 2ac + a^2 ) =0
<=> (a-b)^2 + (b-c)^2 + (c -a)^2 =0 (1)
Vì (a-b)^2 ; (b-c)^2 ; (c -a)^2 ≧ 0 với mọi a,b,c.
=> (a-b)^2 + (b-c)^2 + (c -a)^2 ≧ 0 (2)
Từ (1) và (2) khẳng định dấu "=" khi:
a - b = 0; b - c = 0 ; c - a = 0 => a=b=c
Vậy a=b=c.
Đúng 0
Bình luận (0)
4. Tìm giá trị lớn nhất của các biểu thức a. A = 5 – 8x – x2 b. B = 5 – x2 + 2x – 4y2 – 4y 5. a. Cho a2 + b2 + c2 = ab + bc + ca chứng minh rằng a = b = c b. Tìm a, b, c biết a2 – 2a + b2 + 4b + 4c2 – 4c + 6 = 0 6. Chứng minh rằng: a. x2 + xy + y2 + 1 > 0 với mọi x, y b. x2 + 4y2 + z2 – 2x – 6z + 8y + 15 > 0 Với mọi x, y, z 7. Chứng minh rằng: x2 + 5y2 + 2x – 4xy – 10y + 14 > 0 với mọi x, y.
Bài 1. Cho a2 + b2 + c2 = ab + bc + ca. Chứng minh rằng a = b =c.
\(a^2+b^2+c^2=ab+bc+ca\)
\(\Leftrightarrow2a^2+2b^2+2c^2=2ab+2bc+2ca\)
\(\Leftrightarrow\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ca+a^2\right)=0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-b=0\\b-c=0\\c-a=0\end{matrix}\right.\) \(\Leftrightarrow a=b=c\)
Đúng 3
Bình luận (0)
Ta có: \(a^2+b^2+c^2=ab+bc+ca\)
\(\Leftrightarrow2a^2+2b^2+2c^2-2ab-2bc-2ca=0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
\(\Leftrightarrow a=b=c\)
Đúng 0
Bình luận (0)
a2+b2+c2=ab+bc+caa2+b2+c2=ab+bc+ca
⇔2a2+2b2+2c2=2ab+2bc+2ca⇔2a2+2b2+2c2=2ab+2bc+2ca
⇔(a2−2ab+b2)+(b2−2bc+c2)+(c2−2ca+a2)=0⇔(a2−2ab+b2)+(b2−2bc+c2)+(c2−2ca+a2)=0
⇔(a−b)2+(b−c)2+(c−a)2=0⇔(a−b)2+(b−c)2+(c−a)2=0
⇔⎧⎪⎨⎪⎩a−b=0b−c=0c−a=0⇔{a−b=0b−c=0c−a=0 ⇔a=b=c
Đúng 0
Bình luận (0)