Ai biết thì giúp mình với mình cảm ơn nhiều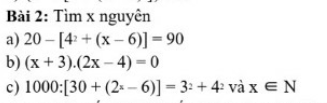

Những câu hỏi liên quan
So sánh cấu trúc lặp xác định được và không xác định được
Có ai biết so sánh thì giúp mình với mình cảm ơn nhiều ạ
giúp mình với mn ai hiểu thì ghi chi tiết cho mình cũng đc! ạ cảm ơn mn nhiều
\(∘ backwin\)
\(CD:1 × 4 = 4 ( c m )\)
\(CR:1 × 3 = 3 ( c m )\)
\(Chiều\) \(cao:1 × 4 = 4 ( c m )\)
\(V: 4 × 3 × 4 = 48 ( c m ^3 )\)
\(Đ/s:48cm^3\)
Đúng 0
Bình luận (1)
Ai giúp mình với !! Mình cảm ơn nhiều
Mình không biết làm câu này nếu ai biết làm ơn chỉ giúp mình, mình cảm ơn nhiều.
Chứng minh x^4-4x+3 không âm với mọi x
câu vừa nãy mình làm sai nha
nếu x = 1 thì phép tính đó âm mất rùi
nên là bài này không có kết quả
Đúng 0
Bình luận (0)
Vì x^4= x.x.x.x
4x+3=x.4+3
=>x^4>4x+3
=>x^4-4x+3>0
=>x^4-4x+3 không âm với mọi x
Đúng 0
Bình luận (0)
X^4-4x+3
=(x^2)^2-2x^2+1+2x^2-4x+2
=(x^2-1)^2+2(x-1)^2 >= 0 với mọi x
vậy x^4-4x+3 không âm với mọi x
Đúng 0
Bình luận (0)
Có bạn nào biết làm thì giúp mình nha mình đanng cần gấp 11 giờ mình phải nộp cho thầy rồi nếu được thì mình cảm ơn nhiều, thầy này kho tính lắm.Nếu được thì mình cảm ơn rất rất nhiều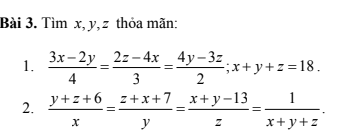
Đây là bài bạn phải nộp cho thầy nên mình sẽ không làm chi tiết. Nhưng mình có thể gợi ý cho bạn như sau:
1.
Đối với tỉ lệ thức đã cho, mỗi phân số ta nhân cả tử và mẫu với 4, 3, 2. Khi đó, ta thu được 1 tỉ lệ thức mới
Dùng tỉ lệ thức trên, áp dụng tính chất dãy tỉ số bằng nhau (cộng), ta thu được $12x=8y=6z(*)$
Tiếp tục áp dụng tính chất dãy tỉ số bằng nhau cho $(*)$ dựa theo điều kiện $x+y+z=18$ ta sẽ tính được $x,y,z$ thỏa mãn.
Đúng 0
Bình luận (0)
2.
Áp dụng tính chất dãy tỉ số bằng nhau (cộng) cho 3 phân số đầu tiên, ta sẽ tìm được tổng $x+y+z$
Khi tìm được tổng $x+y+z$, cộng vào 3 phân số đầu tiên trong bài, mỗi phân số cộng thêm 1. Khi đó, ta thu được tỉ lệ thức $\frac{m}{x}=\frac{n}{y}=\frac{p}{z}(*)$ với $m,n,p$ đã tính được dựa theo giá trị $x+y+z$.
Áp dụng tính chất dãy tỉ số bằng nhau cho tỉ lệ thức $(*)$, kết hợp với kết quả $x+y+z$ thì bài toán đã rất quen thuộc rồi.
Đúng 0
Bình luận (0)
b)áp dụng tính chất dãy tỉ số = nhau ta có:
y+z+6+z+x+7+x+y-13/x+y+z
=2(x+y+z)/x+y+z=2
=>x+y+z=0,5
thay vào bài ta được:
0,5-x+6/x=0,5-y+7/y=0,5-z-13=2
6,5-x/x=7,5-y/y=-12,5-z/z=2
x,y,z tự tính
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
 ai giúp mình với ạ, mình cảm ơn rất nhiều
ai giúp mình với ạ, mình cảm ơn rất nhiều
Gọi điện trở ampe kế là Ra
Hiệu điện thế hai đầu ampe kế A2 là:
\(UA2=I2.Ra=1.Ra=Ra\)
Mà ta lại có: \(UA2=UA3+IA3.2r=IA3.Ra+IA3.2r=0.5Ra+0.5.2r=0.5Ra+r\)
=> \(Ra=0.5Ra+r\)
=> \(r=0.5Ra\)
Ta có: \(IMP=IA2+IA3=1+0.5=1.5\left(A\right)\)
=>\(UMP=IMP.r=1.5r=1,5.0.5Ra=0.75Ra\)
=>\(UMQ=UMP+UA2=0.75Ra+Ra=1.75Ra\)
=> Cường độ dong điện chạy qua ampe kế A1 là:
\(IA1=\dfrac{UMQ}{Ra}=\dfrac{1.75Ra}{Ra}=1.75\left(A\right)\)
Đúng 0
Bình luận (0)
Ai giúp mình bài này với! Mình cảm ơn nhiều.
Ai giúp mình với ạ mình cảm ơn nhiều ạ .
CÂU 1:
\(\dfrac{6x^2y^2}{8xy^5}=\dfrac{3x}{4y^3}\)
CÂU 2:
\(\dfrac{12x^3y^2}{18xy^5}=\dfrac{2x^2}{3y^3}\)
CÂU 3:
\(\dfrac{15x\left(x+5\right)^3}{20x^2\left(x+5\right)}=\dfrac{3\left(x+5\right)^2}{4x}\)
CÂU 4:
\(\dfrac{3xy+x}{9y+3}=\dfrac{x\left(3y+1\right)}{3\left(3y+1\right)}=\dfrac{x}{3}\)
CÂU 5:
\(\dfrac{3xy+3x}{9y+9}=\dfrac{3x\left(y+1\right)}{9\left(y+1\right)}=\dfrac{x}{3}\)
CÂU 6:
\(\dfrac{x^2-xy}{5y^2-5xy}=\dfrac{x\left(x-y\right)}{5y\left(y-x\right)}=\dfrac{-x\left(y-x\right)}{5y\left(y-x\right)}=\dfrac{-x}{5y}\)
CÂU 7:
\(\dfrac{2x^2+2x}{x+1}=\dfrac{2x\left(x+1\right)}{x+1}=2x\)
CÂU 8:
\(\dfrac{7x^2+14x+7}{3x^2+3x}=\dfrac{7\left(x^2+2x+1\right)}{3x\left(x+1\right)}\\ =\dfrac{7\left(x+1\right)^2}{3x\left(x+1\right)}=\dfrac{7\left(x+1\right)}{3x}\)
CÂU 9:
\(\dfrac{10xy^2\left(x+y\right)}{15xy\left(x+y\right)^3}=\dfrac{2y}{3\left(x+y\right)^2}\)
Đúng 0
Bình luận (0)
Ai giúp mình câu này với, mình cảm ơn nhiều 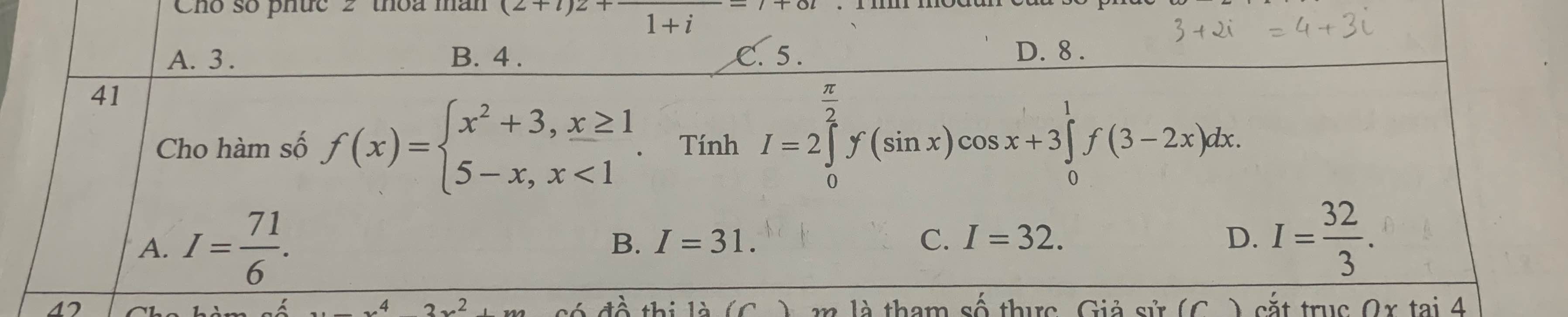
Xét \(I_1=2\int\limits^{\dfrac{\pi}{2}}_0f\left(sinx\right)cosxdx=2\int\limits^{\dfrac{\pi}{2}}_0f\left(sinx\right)d\left(sinx\right)\)
Đặt \(sinx=t\Rightarrow t\in\left[0;1\right]\Rightarrow f\left(t\right)=5-t\)
\(I_1=2\int\limits^1_0\left(5-t\right)dt=9\)
Xết \(I_2=3\int\limits^1_0f\left(3-2x\right)dx=-\dfrac{3}{2}\int\limits^1_0f\left(3-2x\right)d\left(3-2x\right)\)
Đặt \(3-2x=t\Rightarrow t\in\left[1;3\right]\Rightarrow f\left(t\right)=t^2+3\)
\(I_2=-\dfrac{3}{2}\int\limits^1_3\left(t^2+3\right)dt=\dfrac{3}{2}\int\limits^3_1\left(t^2+3\right)dt=22\)
\(\Rightarrow I=9+22=31\)
Đúng 1
Bình luận (0)




















