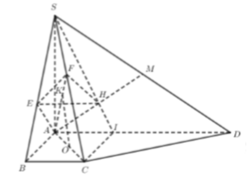
Cho hình chóp S. ABCD có đáy ABCD là hình thang .AD//BC và AD = 2BC .Gọi E và F lần lượt là trung điểm của SA và AD , I là giao điểm của SD và mặt phẳng (BCE). Chứng minh CI // (BEF)

Những câu hỏi liên quan
Cho hình chóp S. ABCD có đáy ABCD là hình thang .AD//BC và AD = 2BC .Gọi E và F lần lượt là trung điểm của SA và AD , I là giao điểm của SD và mặt phẳng (BCE). Chứng minh CI // (BEF)
cho hình chóp s abcd có đáy abcd là hình bình thang AD//BC và AD bằng 2BC gọi E,F lần lượt là trung điểm SA và CD chứng minh CI//(BEF)
Cho hình chóp S.ABCD có đáy ABCD là hình thang ( AD || BC, AD= 2BC ). Gọi M, N lần lượt là trung điểm SA và AB.
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC)
b) Chứng minh MN//(SBC)
c) Gọi O là giao điểm của AC và BD. Xác định thiết diện của hình chóp cắt bởi mặt phẳng (OMN)
a: Xét (SAD) và (SBC) có
\(S\in\left(SAD\right)\cap\left(SBC\right)\)
AD//BC
Do đó: (SAD) giao (SBC)=xy, xy đi qua S và xy//AD//BC
b: Xét ΔSAB có
M,N lần lượt là trung điểm của AS,AB
=>MN là đường trung bình của ΔSAB
=>MN//SB
Ta có: MN//SB
SB\(\subset\)(SBC)
MN ko nằm trong mp(SBC)
Do đó: MN//(SBC)
Đúng 0
Bình luận (0)
Cho hình chóp S.BCD có SA vuông góc với mặt phẳng (ABCD); tứ giác ABCD là hình thang vuông với cạnh đáy AD, BC;
A
D
3
B
C
3
a
;
A
B
a
,
S
A
a
3
. Điểm I thỏa mãn
A
D
⇀
3
A
I...
Đọc tiếp
Cho hình chóp S.BCD có SA vuông góc với mặt phẳng (ABCD); tứ giác ABCD là hình thang vuông với cạnh đáy AD, BC; A D = 3 B C = 3 a ; A B = a , S A = a 3 . Điểm I thỏa mãn A D ⇀ = 3 A I ⇀ ;M là trung điểm SD, H là giao điểm của AM và SI . Gọi E , F lần lượt là hình chiếu của A lên SB , . SC Tính thể tích V của khối nón có đáy là đường tròn ngoại tiếp tam giác EFH và đỉnh thuộc mặt phẳng (ABCD).
A. V = πa 3 2 5
B. V = πa 3 5
C. V = πa 3 10 5
D. V = πa 3 5 5
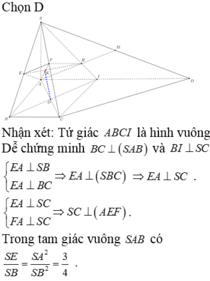
Chọn C.
Phương pháp:
- Chứng minh tứ giác AEFH nội tiếp, từ đó tìm tâm đường tròn ngoại tiếp tam giác EHF .
- Tìm đỉnh hình nón và tính chiều cao, bán kính đáy rồi suy ra thể tích.
Cách giải:
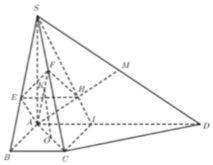



Đúng 0
Bình luận (0)
Cho hình chóp S.BCD có SA vuông góc với mặt phẳng (ABCD); tứ giác ABCD là hình thang vuông với cạnh đáy AD, BC;
A
D
3
B
C
3
a
;
A
B
a
;
S
A
a
3
. Điểm I thỏa mãn
A
D
→...
Đọc tiếp
Cho hình chóp S.BCD có SA vuông góc với mặt phẳng (ABCD); tứ giác ABCD là hình thang vuông với cạnh đáy AD, BC; A D = 3 B C = 3 a ; A B = a ; S A = a 3 . Điểm I thỏa mãn A D → = 3 A I → . M là trung điểm SD, H là giao điểm của AM và SI . Gọi E , F lần lượt là hình chiếu của A lên SB , SC Tính thể tích V của khối nón có đáy là đường tròn ngoại tiếp tam giác EFH và đỉnh thuộc mặt phẳng (ABCD).

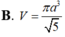
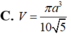
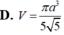
Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD), tứ giác ABCD là hình thang vuông với cạnh đáy AD, BC. AD3CB3a, ABa, SAa
3
. Điểm I thỏa mãn
A
D
→
3
A
I
→
, M là trung điểm SD, H là giao điểm của AM và SI. Gọi E, F lần lượt là hình chiếu của A lên SB, SC. Tính thể tích V của khối nón có đáy là...
Đọc tiếp
Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD), tứ giác ABCD là hình thang vuông với cạnh đáy AD, BC. AD=3CB=3a, AB=a, SA=a 3 . Điểm I thỏa mãn A D → = 3 A I → , M là trung điểm SD, H là giao điểm của AM và SI. Gọi E, F lần lượt là hình chiếu của A lên SB, SC. Tính thể tích V của khối nón có đáy là đường tròn ngoại tiếp tam giác EFH và đỉnh thuộc mặt phẳng (ABCD)
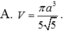
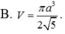
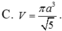
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B,
A
D
2
B
C
,
S
A
⊥
A
B
C
D
.
Gọi E, M lần lượt là trung điểm của AD và SD. K là hình chiếu của E trên SD. Góc giữa (SCD) và (SAD) là: A. góc AMC B. góc EKC C. góc AKC D. góc CSA
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, A D = 2 B C , S A ⊥ A B C D . Gọi E, M lần lượt là trung điểm của AD và SD. K là hình chiếu của E trên SD. Góc giữa (SCD) và (SAD) là:
A. góc AMC
B. góc EKC
C. góc AKC
D. góc CSA
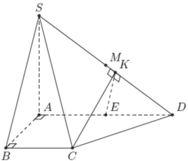
Ta có A E = B C A E / / B C suy ra AECB là hình bình hành. Do A B C ^ = 90 0 nên AECB là hình chữ nhật.
Suy ra C E ⊥ A D mà S A ⊥ C E ⇒ C E ⊥ S A D ⇒ C E ⊥ S D .
Ta lại có E K ⊥ S D ⇒ S D ⊥ E K M ⇒ S D ⊥ C K .
Suy ra góc giữa hai mặt phẳng (SAD) và (SCD) là góc EKC
Đúng 0
Bình luận (0)
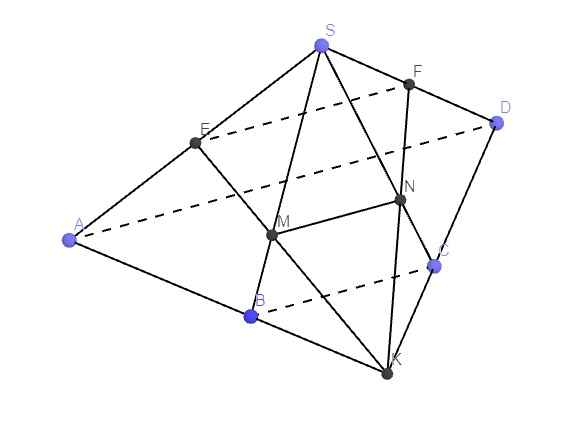
Cho hình chóp S.ABCD, có đáy ABCD là hình thang có đáy lớn AD . Gọi E, F lần lượt là trung điểm của SA, SD.a) Tìm giao tuyến của các cặp mặt phẳng: (SAC) và (SBD), (SAD) và (SBC).b) Chứng minh EF// (ABCD) và EF// (SBC) c) Gọi K là giao điểm của AB và CD. Tìm M, N lần lượt là giao điểm của SB và (CDE); SC và (EFM). Từ đó, tìm thiết diện của hình chóp cắt bởi mặt phẳng (KEF)d) Cho AD2BC. Tính tỉ số diện tích của tam giác KMN và tam giác KEF .giúp mình giải câu d với ạ
Đọc tiếp
Cho hình chóp S.ABCD, có đáy ABCD là hình thang có đáy lớn AD . Gọi E, F lần lượt là trung điểm của SA, SD.
a) Tìm giao tuyến của các cặp mặt phẳng: (SAC) và (SBD), (SAD) và (SBC).
b) Chứng minh EF// (ABCD) và EF// (SBC)
c) Gọi K là giao điểm của AB và CD. Tìm M, N lần lượt là giao điểm của SB và (CDE); SC và (EFM). Từ đó, tìm thiết diện của hình chóp cắt bởi mặt phẳng (KEF)
d) Cho AD=2BC. Tính tỉ số diện tích của tam giác KMN và tam giác KEF .
giúp mình giải câu d với ạ
Áp dụng định lý Talet trong tam giác KAD:
\(\dfrac{KB}{KA}=\dfrac{KC}{KD}=\dfrac{BC}{AD}=\dfrac{1}{2}\)
\(\Rightarrow B,C\) lần lượt là trung điểm AK và DK
Mà E, F là trung điểm SA, SD
\(\Rightarrow\) M, N lần lượt là trọng tâm các tam giác SAK và SDK
\(\Rightarrow\dfrac{SM}{SB}=\dfrac{2}{3}\) ; \(\dfrac{SN}{SC}=\dfrac{2}{3}\)
\(\Rightarrow\dfrac{MN}{BC}=\dfrac{SM}{SB}=\dfrac{SN}{SC}=\dfrac{2}{3}\) (Talet)
\(\Rightarrow MN=\dfrac{2}{3}BC=\dfrac{2}{3}.\dfrac{1}{2}AD=\dfrac{1}{3}AD\)
Lại có EF là đường trung bình tam giác SAD \(\Rightarrow EF=\dfrac{1}{2}AD\)
\(\Rightarrow\dfrac{S_{KMN}}{S_{KEF}}=\dfrac{MN}{EF}=\dfrac{\dfrac{1}{3}AD}{\dfrac{1}{2}AD}=\dfrac{2}{3}\)
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình thang (AD//BC,AD>BC). Gọi M,N,E lần lượt là trung điểm của AB,CD,SA .
a) Chứng minh rằng : (MEN) // (SBC)
b) Trong tam giác SAD vẽ EF // AD (F\(\in\) SD) . Chứng minh rằng F là giao điểm của mặt phẳng (MNE) với SD . Từ đó suy ra thiết diện của hình chóp khi cắt bởi mặt phẳng (MNE) là hình gì ?
Cho tứ diện ABCD . Gọi G1,G2,G3 lần lượt là trọng tâm của các tam giác ABC,ACD,ABD . Chứng minh mặt phẳng (G1G2G3) // (BCD)
Đúng 0
Bình luận (0)