Trong các khẳng định sau, khẳng định nào là sai?
A. \(\left(sinx+cosx\right)^2=1+2sinxcosx\)
B. \(sin^4x+cos^4x=1-2sin^2xcos^2x\)
C. \(\left(sinx-cosx\right)^2=1-2sinxcosx\)
D. \(sin^6x+cos^6x=1-sin^2xcos^2x\)
Cho tam thức f(x) 2x^2-3x+1 . Trong các khẳng định sau , khẳng định nào đúng ?A,f(x) 0 với forall xinleft(dfrac{1}{2};1right) B,fleft(xright)0 với forall xinleft(-infty;1right) C, f(x) 0 với forall xinleft(-infty;1right)cupleft(2;+inftyright) D,f(x) 0 với forall xinleft(-infty;dfrac{1}{2}right)cupleft(1;+inftyright)
Đọc tiếp
Cho tam thức f(x) = \(2x^2-3x+1\) . Trong các khẳng định sau , khẳng định nào đúng ?
A,f(x) > 0 với \(\forall x\in\left(\dfrac{1}{2};1\right)\)
B,\(f\left(x\right)>0\) với \(\forall x\in\left(-\infty;1\right)\)
C, f(x) < 0 với \(\forall x\in\left(-\infty;1\right)\cup\left(2;+\infty\right)\)
D,f(x) >0 với \(\forall x\in\left(-\infty;\dfrac{1}{2}\right)\cup\left(1;+\infty\right)\)
\(\text{f(x)}\)\(\text{>0}\)\(\text{⇔}\)\(\text{2x}\)2\(\text{-3x+1}\)\(>0\)⇔\(\left\{{}\begin{matrix}x>1\\x< \dfrac{1}{2}\end{matrix}\right.\)
⇒x∈(−∞;\(\dfrac{1}{2}\))∪(1;+∞)
Đúng 0
Bình luận (0)
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?a) Nếu điếm P thuộc đường tròn (O; R) thì OP R;b) Nếu điểm P thuộc hình tròn (O; R) thì OP R;c) Nếu điểm P nằm bên trong đường tròn (O; R) thì OP R.
Đọc tiếp
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
a) Nếu điếm P thuộc đường tròn (O; R) thì OP= R;
b) Nếu điểm P thuộc hình tròn (O; R) thì OP < R;
c) Nếu điểm P nằm bên trong đường tròn (O; R) thì OP > R.
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?a) Nếu điếm P thuộc đường tròn (O; R) thì OP R;b) Nếu điểm P thuộc hình tròn (O; R) thì OP R;c) Nếu điểm P nằm bên trong đường tròn (O; R) thì OP R.
Đọc tiếp
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
a) Nếu điếm P thuộc đường tròn (O; R) thì OP = R;
b) Nếu điểm P thuộc hình tròn (O; R) thì OP < R;
c) Nếu điểm P nằm bên trong đường tròn (O; R) thì OP > R.
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?a) Nếu điểm M thuộc hình tròn (O; R) thì OM R;b) Nếu điểm M thuộc đường tròn (O; R) thì OM R;c) Nếu điểm M nằm bên ngoài đường tròn (O; R) thì OM R.
Đọc tiếp
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
a) Nếu điểm M thuộc hình tròn (O; R) thì OM R;
b) Nếu điểm M thuộc đường tròn (O; R) thì OM < R;
c) Nếu điểm M nằm bên ngoài đường tròn (O; R) thì OM > R.
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?a) Nếu điểm M thuộc hình tròn (O; R) thì OM R;b) Nếu điểm M thuộc đường tròn (O; R) thì OM R;c) Nếu điểm M nằm bên ngoài đường tròn (O; R) thì OM R.
Đọc tiếp
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
a) Nếu điểm M thuộc hình tròn (O; R) thì OM = R;
b) Nếu điểm M thuộc đường tròn (O; R) thì OM < R;
c) Nếu điểm M nằm bên ngoài đường tròn (O; R) thì OM > R.
trong mặt phẳng oxy, cho đường tròn \(\left(C_m\right):x^2+y^2-4x-6y=m-12\) và đường thẳng \(d:2x+y-2=0\). Biết rằng (Cm) cắt d theo một dây cung có độ dài bằng 2. khẳng định nào dưới đây đúng?
A. \(m\in\left(3\sqrt{2};6\right)\)
B. m < 2
C. \(m\in\left(2;3\right)\)
D. m > 8
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai? Với khẳng định sai, hãy sửa lại cho đúng.
a) ƯC(12, 24) = {1; 2; 3; 4; 6; 8; 12};
b) ƯC(36, 12, 48) = {1; 2; 3; 4; 6; 12}.
a) Sai vì 8 không là ước chung của 12 và 24
Sửa lại:
Ư(12) = {1; 2; 3; 4; 6; 12}
Ư(24) = {1; 2; 3; 4; 6; 8; 12; 24}
=> ƯC(12, 24) = {1; 2; 3; 4; 6; 12}
b) Đúng.
Ư(36) = {1; 2; 3; 4; 6; 9; 12; 18; 36}
Ư(12) = {1; 2; 3; 4; 6; 12}
Ư(48) = {1; 2; 3; 4; 6; 12; 24; 48}
=> ƯC(36, 12, 48) = {1; 2; 3; 4; 6; 12}.
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho ba điểm A(0; 0; 0), B(1; 2; 3), C(2; 3; 1). Gọi D là chân đường phân giác trong xuất phát từ đỉnh A của tam giác ABC. Trong các khẳng định dưới đây, khẳng định nào sai? A. AD ⊥ BC B. Một vectơ chỉ phương của đường thẳng AD là:
AB
→
+
AC
→
C. Một vectơ chỉ phương của đường thẳng AD là: D. Một vectơ chỉ phương của đường thẳng AD là: ...
Đọc tiếp
Trong không gian Oxyz, cho ba điểm A(0; 0; 0), B(1; 2; 3), C(2; 3; 1). Gọi D là chân đường phân giác trong xuất phát từ đỉnh A của tam giác ABC. Trong các khẳng định dưới đây, khẳng định nào sai?
A. AD ⊥ BC
B. Một vectơ chỉ phương của đường thẳng AD là: AB → + AC →
C. Một vectơ chỉ phương của đường thẳng AD là: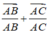 
D. Một vectơ chỉ phương của đường thẳng AD là: u AD → = (1; 1; -2)
Đáp án D
Ta có:
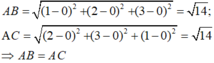
Ta thấy tam giác ABC cân tại đỉnh A. Do đó, AD đồng thời là đường cao của tam giác ABC nên các khẳng định A, B và C đều đúng.
Vậy khẳng định D sai.
Đúng 0
Bình luận (0)
Cho đường tròn (C):
x
2
+
y
2
- 4x + 2y + 1 0 và đường thẳng d: 3x + y + 1 0. Trong các khẳng định sau, khẳng định nào đúng? A. Đường thẳng d cắt đường tròn (C) tại hai điểm phân biệt (không đi qua tâm) B. Đường thẳng d tiếp xúc với đường tròn (C) C. Đường thẳng d không cắt đường tròn (C) D. Đường thẳng d đi qua tâm của đường tròn (C)
Đọc tiếp
Cho đường tròn (C): x 2 + y 2 - 4x + 2y + 1 = 0 và đường thẳng d: 3x + y + 1 = 0. Trong các khẳng định sau, khẳng định nào đúng?
A. Đường thẳng d cắt đường tròn (C) tại hai điểm phân biệt (không đi qua tâm)
B. Đường thẳng d tiếp xúc với đường tròn (C)
C. Đường thẳng d không cắt đường tròn (C)
D. Đường thẳng d đi qua tâm của đường tròn (C)
Đáp án: A
Ta có:
(C): x 2 + y 2 - 4x + 2y + 1 = 0 ⇔ (x - 2 ) 2 + (y + 1 ) 2 = 4
⇒ I(2;-1), R = 2
Ta thấy:
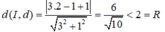
Suy ra, d cắt đường tròn (C) tại hai điểm phân biệt
Thay tọa độ của I vào vế trái phương trình đường thẳng d ta được: 3.2 - 1 + 1 = 6 ≠ 0
Suy ra, I không thuộc d
Đúng 0
Bình luận (0)