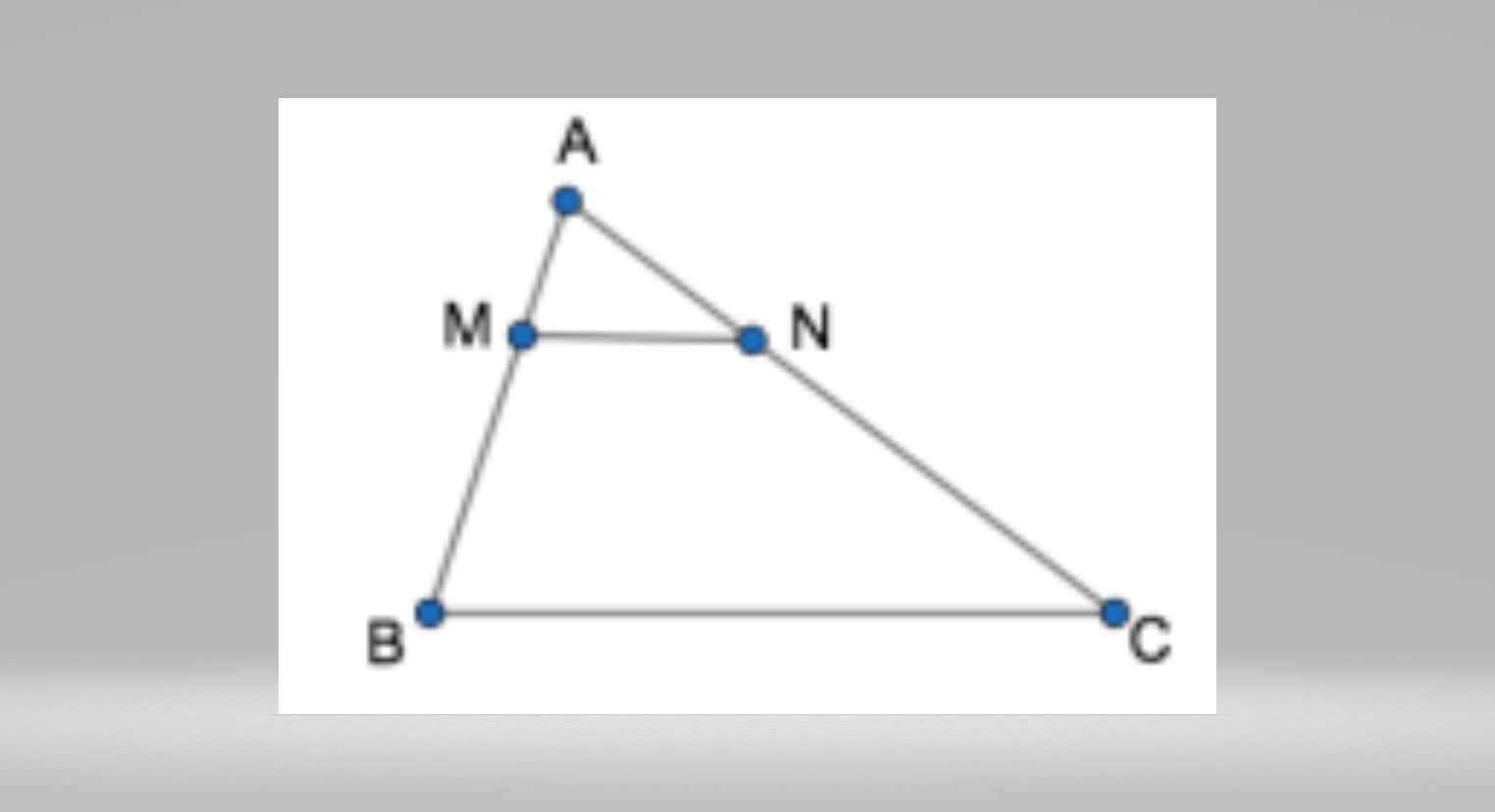
Cho tam giác ABC như hình vẽ
bên. BiếtAM=1/3 x AB; AN = 1/3 x AC và diện
tích tam giác AMN là 6cm2. Tính diện
tích tam giác ABC.
 kho qua !!!!!11 giup minh nha!!
kho qua !!!!!11 giup minh nha!!
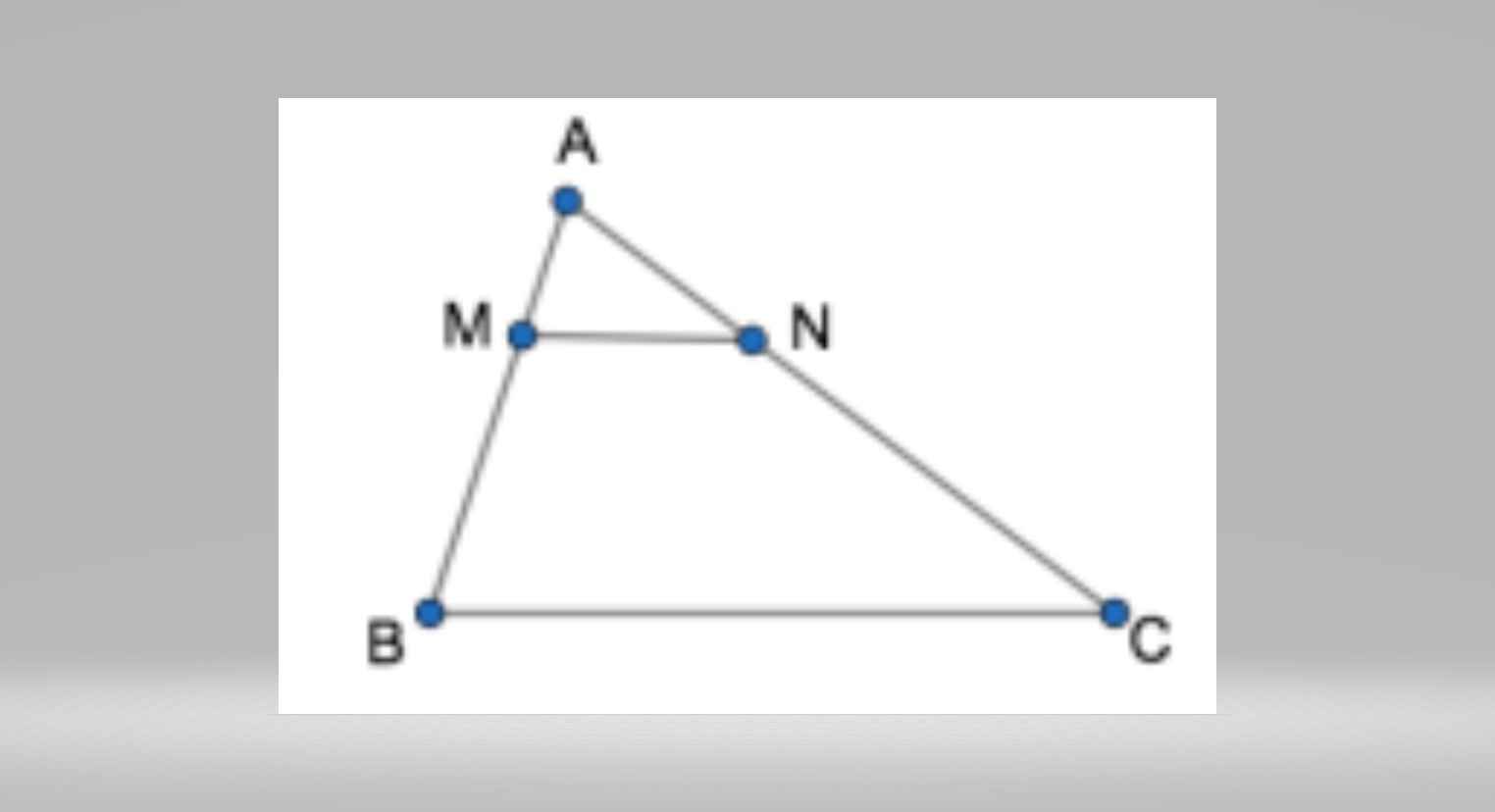
Cho tam giác ABC như hình vẽ
bên. Biết AM= 1/3 x AB; AN = 1/3 AC và diện
tích tam giác AMN là 6cm2. Tính diện
tích tam giác ABC.
 KHO QUAAAAA
KHO QUAAAAA
Bài 10: Cho hình thang BPQC ( như hình vẽ).
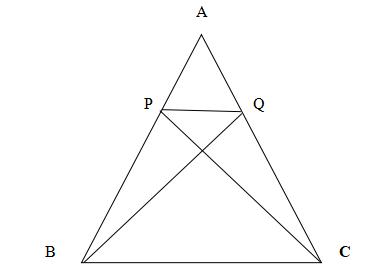
a) So sánh diện tích tam giác BIP và tam giác QIC.
b) Tính diện tích BPQC biết AP = 1/3 AB và diện tích tam giác ABC= 45 cm2.
a/
Hai tg BPQ và tg CQP có đường cao từ B->PQ = đường cao từ C->PQ
Cạnh đáy PQ chung
\(\Rightarrow S_{BPQ}=S_{CQP}\)
Hai tg trên có phần diện tích chung là \(S_{IPQ}\Rightarrow S_{BIP}=S_{QIC}\)
b/
Hai tg ACP và tg ABC có chung đường cao từ C->AB nên
\(\dfrac{S_{ACP}}{S_{ABC}}=\dfrac{AP}{AB}=\dfrac{1}{3}\Rightarrow S_{ACP}=\dfrac{1}{3}xS_{ABC}\)
Hai tg ACP và tg ABQ có phần diện tích chung là \(S_{APIQ}\)
Mà \(S_{BIP}=S_{QIC}\Rightarrow S_{ACP}=S_{ABQ}=\dfrac{1}{3}xS_{ABC}\)
Hai tg APQ và tg ABQ có chung đường cao từ Q->AB nên
\(\dfrac{S_{APQ}}{S_{ABQ}}=\dfrac{AP}{AB}=\dfrac{1}{3}\Rightarrow S_{APQ}=\dfrac{1}{3}xS_{ABQ}=\dfrac{1}{3}x\dfrac{1}{3}xS_{ABC}=\dfrac{1}{9}xS_{ABC}\)
\(\Rightarrow S_{BPQC}=S_{ABC}-S_{APQ}=S_{ABC}-\dfrac{1}{9}xS_{ABC}=\dfrac{8}{9}xS_{ABC}=\dfrac{8}{9}x45=40cm^2\)
cho tam giác ABC có cạnh BC = 7,2 cm và chiều cao vẽ từ A bằng 7,5 cm (như hình vẽ ) a,tính diện tích tam giác ABC
B, trên AB lấy điểm P sao cho AP = 2/3 AB , trên AC lấy điểm Q sao cho AQ = 1/4 AC . tính diện tính tam giác APQ
bn tham khảo:
a) Diện tich tam giác ABC là :
7,2 x 7,5 : 2 = 27 ( cm2 )
b) Nối P với C
Xét hai tam giác APC và ABC
Chung chiều cao hạ từ đỉnh C xuống cạnh AB
PA = 2/3 AB
=> SAPC = SABC x 2/3 = 27 x 2/3 = 18 ( cm2 )
Xét 2 tam giác APQ và APC
Chung chiều cao hạ từ đỉnh P xuống cạnh AC
AQ = 1/4 AC
=> SAPQ = SAPC X 1/4 = 18 x 1/4 = 4,5 ( cm2 )
Đáp số : 4,5 cm2
Cho tam giác ABC ( như hình vẽ )AM bằng 1/3 AB , AN bằng 1/3 AC .
a,Hãy tìm trong hình vẽ những cặp tam giác bằng nhau và giải thích .
b,Tính S tứ giác BMNC biết S tam giác ABC là 36 cm vuông
ai nhanh nhất mà có bài giải thì mik tick cho.
Cho hình tam giác ABC. Trên cạnh AB lấy điểm M, trên AC lấy điểm N sao cho AM=1/3 AB, NC=2/3 AC. Diện tích hình tam giác ABC gấp diện tích hình tam giác AMN ..... lần
Cho tam giác ABC. Lấy M,N làn lượt trên AB và AC sao cho AM = 1/2 AB, AN = 1/3 AC. Tính diện tích hình tam giác AMN biết diện tích hình tam giác ABC là 27cm2.
\(AM=\dfrac{1}{2}AB\)
=>\(S_{AMC}=\dfrac{1}{2}\cdot S_{ABC}=\dfrac{1}{2}\cdot27=13,5\left(cm^2\right)\)
Vì \(AN=\dfrac{1}{3}AC\)
nên \(S_{AMN}=\dfrac{1}{3}\cdot S_{AMC}=\dfrac{1}{3}\cdot13,5=4,5\left(cm^2\right)\)
1) Cho hình tam giác ABC có AD = 1/3 AC, BE = 1/2 BD, diện tích hình tam giác EBC là 1,2 cm2. Tính diện tích hình tam giác ABC.
2)Cho hình tam giác vuông ABC có AB = 3cm, AC = 4cm. Trên các cạnh của hình tam giác ABC có BG = 1/2 BC; BD = 1/3 BA; AE = 1/4 AC. Tính diện tích hình tam giác DEG.
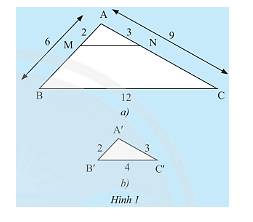
Cho tam giác \(ABC\) và tam giác \(A'B'C'\) có các kích thước như Hình 1. Trên cạnh \(AB\) và \(AC\) của tam giác \(ABC\) lần lượt lấy hai điểm \(M,N\) sao cho \(Am = 2cm,AN = 3cm\).
a) So sánh các tỉ số \(\frac{{A'B'}}{{AB}},\frac{{A'C'}}{{AC}},\frac{{B'C'}}{{BC}}\).
b) Tính độ dài đoạn thẳng \(MN\).
c) Em có nhận xét gì về mối liên hệ giữ các tam giác \(ABC,AMN\) và \(A'B'C'\)?
a) Ta có: \(\frac{{A'B'}}{{AB}} = \frac{2}{6} = \frac{1}{3},\frac{{A'C'}}{{AC}} = \frac{3}{9} = \frac{1}{3},\frac{{B'C'}}{{BC}} = \frac{4}{{12}} = \frac{1}{3}\). Do đó, các tỉ số trên bằng nhau.
b) Ta có: \(\frac{{AM}}{{AB}} = \frac{2}{6} = \frac{1}{3};\frac{{AN}}{{AC}} = \frac{3}{9} = \frac{1}{3}\)
Vì \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} \Rightarrow MN//BC\) (định lí Thales đảo)
Vì \(MN//BC \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\) (Hệ quả của định lí Thales)
Do đó, \(\frac{{MN}}{{BC}} = \frac{1}{3} \Leftrightarrow \frac{{MN}}{{12}} = \frac{1}{3} \Rightarrow MN = \frac{{12.1}}{3} = 4\).
Vậy \(MN = 4cm\).
c) Vì \(MN//BC \Rightarrow \Delta ABC\backsim\Delta AMN\) (định lí)(1)
Xét tam giác \(AMN\) và tam giác \(A'B'C'\) ta có:
\(AM = A'B' = 2cm;AN = A'C' = 2cm;MN = B'C' = 4cm\)
Do đó, \(\Delta AMN = \Delta A'B'C'\) (c.c.c)
Vì \(\Delta AMN = \Delta A'B'C'\) nên \(\Delta AMN\backsim\Delta A'B'C'\) (2)
Từ (1) và (2) suy ra, \(\Delta ABC\backsim\Delta A'B'C'\).
cho hình tam giác ABC .trên BC lấy điểm D sao cho CD =1/3 BC. Trên AB lấy điểm E sao cho BE = AB. Nối E với D, biết diện tích hình tam giác BED là 9cm2. Tính diện tích hình tam giác ABC
ABD và BDE có Ab=BE , và có chung cạnh BD
=> ABD =BED =9cm2
DC=1/3 BC => DC=1/2 BD
ABD và ACD có DC=1/2 BD và chung đường cao hạ từ đỉnh C
=> ADC = 1/2 ABD = 1/2x9=4,5cm2
=> S. ABC = 9+4,5=13,5cm2