tìm a và b biết đường thẳng ax+by=-2 đi qua 2 điểm A(2;-12) và B(-1;2)

Những câu hỏi liên quan
tìm 2 số a và b sao cho 5a - 4b =-5 và đường thẳng ax + by =-1 đi qua điểm A(-7,4)
Tìm các giá trị của a và b để đường thẳng ax-by=4 đi qua 2 điểm A(4:3) và B(-6:-7)
Vì đường thẳng ax-by=4 đi qua 2 điểm A(4;3) và B(-6;-7)
nên 4a-3b=4 và -6a-(-7)b=4
3(4a-3b)=12 và 2(-6a+7b)=8
12a-9b=12 và -12a+14b=8
5b=20 và 4a-3b=4
b=4 và a=4
Bài 6. Trong hệ trục tọa độ Oxy, biết đường thẳng y = ax + b đi qua điểm A(2;3) và điểm B(-2;1) Tìm các hệ số a và b.
Bài 7. Viết phương trình đường thẳng (d) đi qua 2 điểm A(1; 2) và B(2; 0).
TÌM CÁC GIÁ TRỊ A,B BIẾT :
A) ax+by =1 đi qua a(-2;1)và b (3;-2)
b) đường thẳng 3ax+2by=5 đi qua m(-1;2)và vuông góc đường thẳng 2x+3y=1
Tìm 2 số a và b sao cho 5a-4b=-5 và đường thẳng ax+by=-1 đi qua điểm A_(-7;4)
Biết đường thẳng y = ax+b đi qua điểm M (2;\(\dfrac{1}{2}\)) và song song với đường thẳng y = 2x+3. Tìm hệ số a và b
Gọi (d): y = ax + b
(d'): y = 2x + 3
Do (d) // (d') nên a = 2
(d): y = 2x + b
Thay tọa độ điểm M(2; 1/2) vào (d) ta được:
2.2 + b = 1/2
b = 1/2 - 4
b = -7/2
Vậy a = 2; b = -7/2
Đúng 1
Bình luận (0)
d//y=2x+3 nên a=2
=>y=2x+b
Thay x=2 và y=1/2 vào (d), ta được:
b+1=1/2
=>b=-1/2
Đúng 1
Bình luận (0)
I)Trong mặt phẳng tọa độ Oxy cho hàm số y=ax*2 có đồ thị (P)
1/Tìm a, biết rằng (P) cắt đường thẳng (d) có phương trình y=-x-3/2 tại điểm A có hoành độ bằng 3. Vẽ đồ thị P ứng với a vừa tìm được.
2/ Tìm tọa độ giao điểm thứ 2 B (khác A) của (P) và (d)
II)Tìm 2 số a,b sao cho 7a+6b=-4 và đường thẳng ax+by=-1 đi qua điểm A(-2;-1)
a) (d) cắt (P) tại A => A thuộc d và (P)
xA= 3; A \(\in\) d=> yA = -xA - \(\frac{3}{2}\) => yA = -3 - \(\frac{3}{2}\) = \(\frac{-9}{2}\)
Mặt khác, A \(\in\) (P) => yA = axA2 => \(\frac{-9}{2}\) = a. 32 => a = \(\frac{-9}{2}\): 9 = \(\frac{-1}{2}\)
Vậy (P) có dạng y = \(\frac{-1}{2}\).x2
+) Vẽ đồ thị:
| x | -2 | -1 | 0 | 1 | 2 |
| y | -2 | \(\frac{-1}{2}\) | 0 | \(\frac{-1}{2}\) | -2 |
(P) đí qua 4 điểm (-2;-2); (-1;\(\frac{-1}{2}\)); (0;0); (1;\(\frac{-1}{2}\)); (2;-2)
b) Phương trình hoành độ giao điểm: \(\frac{-1}{2}\).x2 = - x - \(\frac{3}{2}\)
<=> -x2 + 2x + 3 = 0
<=> x = -1 hoặc x = 3 (Vì a - b + c = -1 - 2 + 3 = 0)
=> xB = -1 => yB = \(\frac{-1}{2}\).(-1)2 = \(\frac{-1}{2}\)
Vậy B (-1;\(\frac{-1}{2}\))
Đúng 0
Bình luận (0)
Tìm a , b biết đường thẳng y = ax + b
Đi qua điểm M(2 ; 3) và N(-1 ; 4)
Vì (d) đi qua M(2;3) và N(-1;4) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}2a+b=3\\-a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3a=-1\\-a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{1}{3}\\b=a+4=4-\dfrac{1}{3}=\dfrac{11}{3}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Tìm giao điểm của hai đường thẳng: (
d
1
): ax + 2y -3 và (
d
2
): 3x – by 5, biết rằng (
d
1
) đi qua điểm M(3; 9) và (
d
2
) đi qua điểm N(-1; 2).
Đọc tiếp
Tìm giao điểm của hai đường thẳng:
( d 1 ): ax + 2y = -3 và ( d 2 ): 3x – by = 5, biết rằng ( d 1 ) đi qua điểm M(3; 9) và ( d 2 ) đi qua điểm N(-1; 2).
*Đường thẳng ( d 1 ): ax + 2y = -3 đi qua điểm M(3; 9) nên tọa độ điểm M nghiệm đúng phương trình đường thẳng.
Ta có: a.3 + 2.9 = -3 ⇔ 3a + 18 = -3 ⇔ 3a = -21 ⇔ a = -7
Phương trình đường thẳng ( d 1 ): -7x + 2y = -3
*Đường thẳng ( d 2 ): 3x – by = 5 đi qua điểm N(-1; 2) nên tọa độ điểm N nghiệm đúng phương trình đường thẳng.
Ta có: 3.(-1) – b.2 = 5 ⇔ -3 – 2b = 5 ⇔ 2b = -8 ⇔ b = -4
Phương trình đường thẳng ( d 2 ): 3x + 4y = 5
*Tọa độ giao điểm của (
d
1
) và (
d
2
) là nghiệm của hệ phương trình: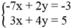
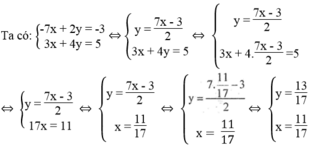
Đúng 0
Bình luận (0)
















