CHHỨNG MINH: a) MN= PQ b)MP// NQ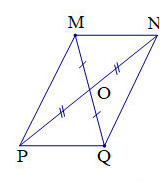

Những câu hỏi liên quan
Cho hình bs.9. Khi đó
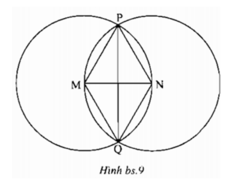
(A) MP = MQ = MN = PQ;
(B) MP = MQ = NQ = NP;
(C) MP = MQ = NP = PQ;
(D) MP = MQ > NQ = NP;
Cho hình thang MNPQ (MN // PQ) có MP = NQ. Qua N kẻ đường thảng song song vói MP, cắt đường thẳng PQ tại K chứng minh: tam giác NKQ là tam giác cân cho hình thang MNPQ ( MN song song PQ) có MP = NQ . Qua N kẻ đường thảng song song vs MP , cắt đường thẳng PQ tại Kchứng minh: a) tam giác NKQ là tam giác cân b) tam giác MPQ = tam giác NQP c) MNPQ lằ hình thang cân
a: Xét tứ giác MNKP có
MN//KP
MP//NK
=>MNKP là hình bình hành
=>MP=NK
mà MP=NQ
nên NK=NQ
=>ΔNKQ cân tại N
b: MNKP là hbh
=>góc K=góc NMP
=>góc K=góc MPQ
=>góc MPQ=góc NQP
Xét ΔMQP và ΔNPQ có
MP=NQ
góc MPQ=góc NQP
QP chung
=>ΔMQP=ΔNPQ
c: ΔMQP=ΔNPQ
=>góc MQP=góc NPQ
=>MNPQ là hình thang cân
Đúng 3
Bình luận (0)
Cho hình thang MNPQ (MN // PQ ), có O là giao điểm 2 đường chéo MP và NQ.
Đường thẳng song song với MN cắt MQ, NQ, MP, NP lần lượt tại A, B, C, D.
a) Chứng minh OM . OB = ON . OC
b) Chứng minh AB = CD
Cho hình bình hành MNPQ ( MN NP). Kẻ MN vuông góc với NQ ( H thuộc NQ), kẻ PK vuông góc với NQ ( K thuộc NQ)a) chứng minh MHPK b) Chứng minh tứ giác MKPH là hình bình hành c) Gọi O là giao điểm của MP và NQ. Tia MH cắt PQ tại E, tia PK cắt MN tại F. Chứng minh E,O,F thẳng hàng.
Đọc tiếp
Cho hình bình hành MNPQ ( MN > NP). Kẻ MN vuông góc với NQ ( H thuộc NQ), kẻ PK vuông góc với NQ ( K thuộc NQ)
a) chứng minh MH=PK
b) Chứng minh tứ giác MKPH là hình bình hành
c) Gọi O là giao điểm của MP và NQ. Tia MH cắt PQ tại E, tia PK cắt MN tại F. Chứng minh E,O,F thẳng hàng.
a: Xét ΔMHQ vuông tại H và ΔPKN vuông tại K có
MQ=PN
\(\widehat{MQH}=\widehat{PNK}\)
Do đó: ΔMHQ=ΔPKN
Suy ra: MH=PK
Đúng 0
Bình luận (0)
cho 2 đường thẳng a b song song nhau. trên đường thẳng a lấy 2 điểm M,N và trên đường thẳng b lấy P,Q sao cho MN=PQ. nối M với P và N với Q
a) chứng minh MP=NQ
b) chứng minh MP||NQ
a)Kẻ NP
Ta có:
a//b
=> MNP=NPQ(so le trong)
Xét \(_{\Delta MPN}\) và \(\Delta QNP\) có:
MNP=NPQ( cmt)
NP là cạnh chung
MN=QP
=)\(\Delta MNP=\Delta QNP\)(C-g-C)(1)
=>MPN=QNP(hai cạnh tương ứng)
Mà hai góc này ở vị trí so le trong => MP//NQ(dpcm)
b) Từ (1) => MP=NP(dpcm)
CHÚC BẠN HỌC TỐT!
Đúng 0
Bình luận (0)
a) ta có a//b suy ra MN//PQ suy ra góc MNP = góc NPQ (hai góc so le trong)
xét tam giác MNP và tam giác QPN ta có
MN=QP
góc MNP= góc QPN
NP:cạnh chung
suy ra tam giác MNP= tam giác QPN(c.g.c)
suy ra MP=NQ(hai cạnh tương ứng)
b)ta có tam giác MNP= tam giác QPN suy ra góc MPN=góc QNP(hai góc tương ứng)
mà hai góc này ở vị trí so le trong suy ra MP//NQ(đpcm)
Đúng 0
Bình luận (0)
Cho 2 đoạn thẳng MN và PQ cắt nhau tại trung điểm E của mỗi đoạn
a, Chứng minh: MP = NQ
b, Chứng minh: MQ = NP
c, Chứng minh: MP // NQ
a: Xét tứ giác MPNQ có
E là trung điểm của MN
E là trung điểm của QP
Do đó: MPNQ là hình bình hành
Suy ra: MP=NQ
b: Ta có: MPNQ là hình bình hành
nên MQ=NP
c: Ta có: MPNQ là hình bình hành
nên MP//NQ
Đúng 1
Bình luận (0)
Cho tứ giác lồi MNPQ có 2 đường chéo cắt nhau tại O.
a) Chứng minh 2NO > MN + NP - MP
b) Giả sử MN + NQ \(\le\)MP + PQ
CHứng minh MN < MP
Cho 2 đoạn thẳng MN và PQ cắt nhau tại O. Nối M với P ,N với Q
a, Tính tổng các góc MPN,MQN,PMQ,PNQ\
b, So sánh MN+PQ voi MQ+NP,MP+NQ
MN+PQvoi MP+NQ+MQ+NP
Cho tứ giác lồi MNPQ có 2 đường chéo cắt nhau tại O.
a) Chứng minh 2NO > MN + NP - MP
b) Giả sử MN + NQ \(\le\)MP + PQ
CHứng minh MN < MP















