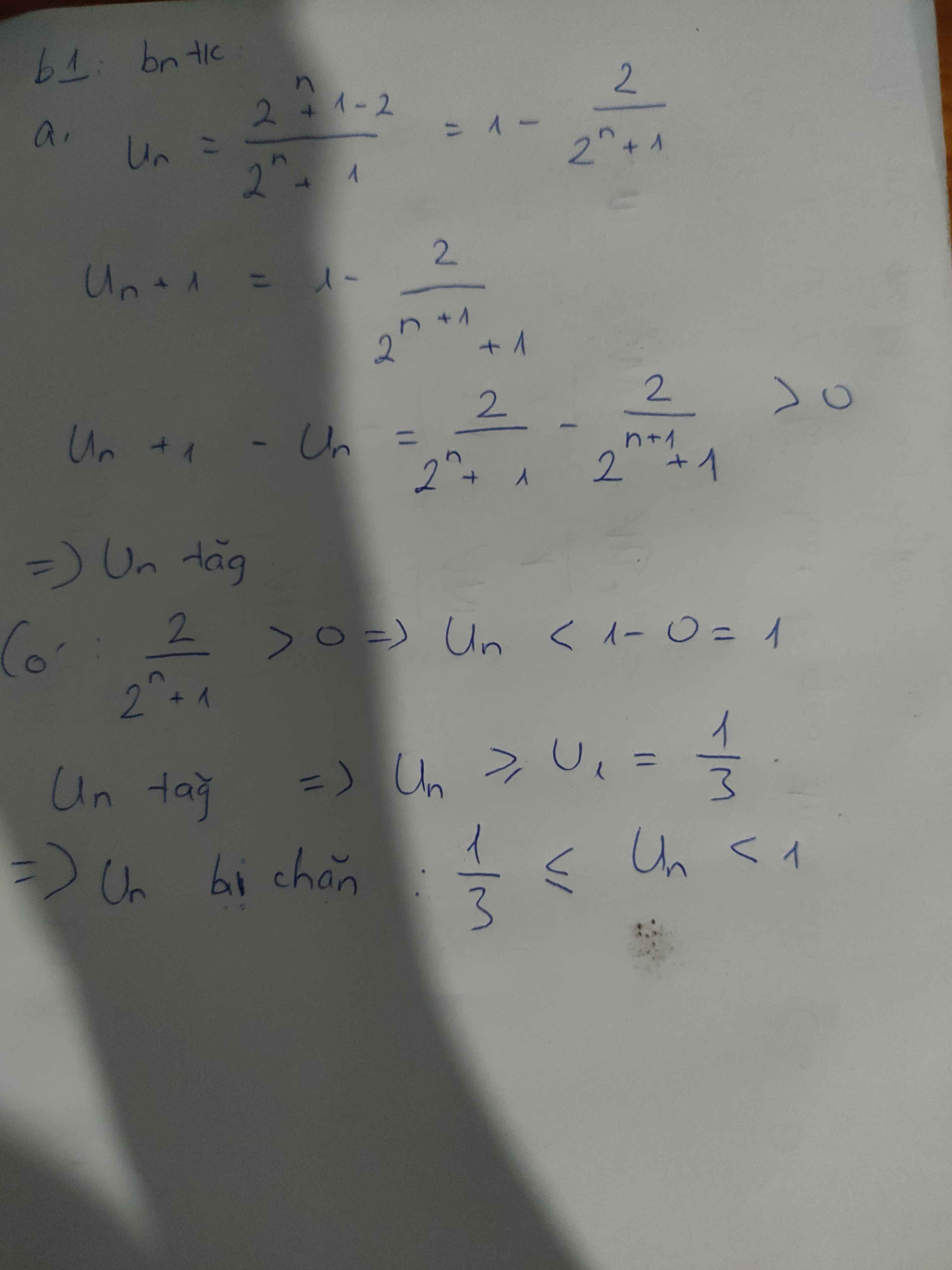Xét tính bị chặn của un=1/(n+1)

Những câu hỏi liên quan
Xét tính bị chặn của un
•un= 5/(n²+1) + (n+2)/(n+1) + cos(n)
•un=1/(n²+1) + sin(n)
Xét tính tăng, giảm, bị chặn của dãy số (un) với un = 1/n+1
\(u_n=\dfrac{1}{n+1}\Rightarrow u_{n+1}=\dfrac{1}{n+2}\)
\(\Rightarrow u_n-u_{n+1}=\dfrac{1}{n+1}-\dfrac{1}{n+2}=\dfrac{1}{\left(n+1\right)\left(n+2\right)}>0\)
\(\Rightarrow u_{n+1}< u_n\Rightarrow\) dãy giảm
Do \(\dfrac{1}{n+1}>0\Rightarrow\) dãy bị chặn dưới bởi 0
\(u_n-1=\dfrac{1}{n+1}-1=-\dfrac{n}{n+1}< 0\Rightarrow u_n< 1\)
\(\Rightarrow\) Dãy bị chặn trên bởi 1
\(\Rightarrow\) Dãy bị chặn
Đúng 1
Bình luận (0)
Bài 1: Xét tính tăng giảm của các dãy số (Un) với
a)\(Un=\dfrac{2^n-1}{2^n+1}\) b)\(Un=\left(-1\right)^n.n\)
Bài 2: Xét tính bị chặn của
\(Un=\sqrt[3]{n}-\sqrt[3]{n+1}\)
Xét tính tăng, giảm và bị chặn của các dãy số u n , biết: u n = n + 1 - n
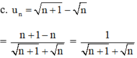
+ Xét tính tăng giảm.
Với mọi n ∈ N ta có:
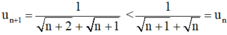
⇒ un + 1 < un với mọi n ∈ N.
⇒ (un) là dãy số giảm.
+ Xét tính bị chặn.
un > 0 với mọi n.
⇒ (un) bị chặn dưới.
un ≤ u1 = √2 - 1 với mọi n
⇒ (un) bị chặn trên.
⇒ (un) bị chặn.
Đúng 0
Bình luận (0)
Xét tính bị chặn của các dãy số sau:
u
n
(
-
1
)
n
A. Bị chặn B. Không bị chặn C. Bị chặn trên D. Bị chặn dưới
Đọc tiếp
Xét tính bị chặn của các dãy số sau: u n = ( - 1 ) n
A. Bị chặn
B. Không bị chặn
C. Bị chặn trên
D. Bị chặn dưới
xét tính bị chặn của dãy số un=\(n^2-\sqrt{n^2+1}\)
Bạn xem lại xem viết đề có thiếu/nhầm gì không?
Đúng 1
Bình luận (0)
Xét tính tăng giảm và bị chặn của dãy số sau: (un)
u
1
2
u
n
+
1
u
n...
Đọc tiếp
Xét tính tăng giảm và bị chặn của dãy số sau: (un) u 1 = 2 u n + 1 = u n + 1 2 , ∀ n ≥ 2
A. Tăng, bị chặn
B. Giảm, bị chặn
C. Tăng, chặn dưới
D. Giảm, chặn trên
Chọn B.
Trước hết bằng quy nạp ta chứng minh: (un) 1 < un ≤ 2, ∀ n
Điều này đúng với n = 2, giả sử 1 < un < 2 ta có: ![]() nên ta có đpcm.
nên ta có đpcm.
Mà ![]() .
.
Vậy dãy (un) là dãy giảm và bị chặn.
Đúng 0
Bình luận (0)
Xét tính tăng giảm và bị chặn của các dãy số sau:
u
1
2
;
u
2
3
u
n...
Đọc tiếp
Xét tính tăng giảm và bị chặn của các dãy số sau: u 1 = 2 ; u 2 = 3 u n + 1 = u n + u n - 1 , ∀ n ≥ 2
A. Tăng, bị chặn
B. Giảm, bị chặn
C. Tăng, chặn dưới
D. Giảm, chặn trên
Chọn A.
Trước hết ta chứng minh 1 < un < 4
Điều này hiển nhiên đúng với n = 1.
Giả sử 1 < un < 4, ta có: ![]()
Ta chứng minh (un) là dãy tăng
Ta có u1 < u2, giả sử un-1 < un, ∀ n ≤ k.
Khi đó: 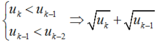
![]()
Vậy dãy (un) là dãy tăng và bị chặn.
Đúng 0
Bình luận (0)
Cho dãy số (Un), với un = 1/1×2+ 1/2×3 + 1/3×4 +...+ 1/n(n+1). Xét tính tăng, giảm và bị chặn của dãy số.
\(u_n=\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{n\left(n+1\right)}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{n}-\dfrac{1}{n+1}\)
\(=1-\dfrac{1}{n+1}< 1\)
=>Hàm số bị chặn trên tại \(u_n=1\)
\(n+1>=1\)
=>\(\dfrac{1}{n+1}< =1\)
=>\(-\dfrac{1}{n+1}>=-1\)
=>\(1-\dfrac{1}{n+1}>=-1+1=0\)
=>Hàm số bị chặn dưới tại 0
\(u_n=1-\dfrac{1}{n+1}=\dfrac{n+1-1}{n+1}=\dfrac{n}{n+1}\)
\(\dfrac{u_n}{u_{n+1}}=\dfrac{n}{n+1}:\dfrac{n+1}{n+2}=\dfrac{n^2+2n}{n^2+2n+1}< 1\)
=>(un) là dãy số tăng
Đúng 1
Bình luận (0)