Chọn A.
Trước hết ta chứng minh 1 < un < 4
Điều này hiển nhiên đúng với n = 1.
Giả sử 1 < un < 4, ta có: ![]()
Ta chứng minh (un) là dãy tăng
Ta có u1 < u2, giả sử un-1 < un, ∀ n ≤ k.
Khi đó: 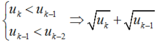
![]()
Vậy dãy (un) là dãy tăng và bị chặn.
Chọn A.
Trước hết ta chứng minh 1 < un < 4
Điều này hiển nhiên đúng với n = 1.
Giả sử 1 < un < 4, ta có: ![]()
Ta chứng minh (un) là dãy tăng
Ta có u1 < u2, giả sử un-1 < un, ∀ n ≤ k.
Khi đó: 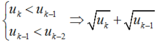
![]()
Vậy dãy (un) là dãy tăng và bị chặn.
Cho dãy số (Un), với un = 1/1×2+ 1/2×3 + 1/3×4 +...+ 1/n(n+1). Xét tính tăng, giảm và bị chặn của dãy số.
Xét tính tăng giảm và bị chặn của dãy số sau: (un) u 1 = 2 u n + 1 = u n + 1 2 , ∀ n ≥ 2
A. Tăng, bị chặn
B. Giảm, bị chặn
C. Tăng, chặn dưới
D. Giảm, chặn trên
Xét tính tăng, giảm và bị chặn của các dãy số u n , biết: u n = n + 1 - n
Chứng minh dãy số (un) với \(u_n=\sqrt{n^2+2}-n\) là dãy số giảm và bị chặn
Xét tính tăng hay giảm và bị chặn của dãy số : u n = 2 n − 1 n + 3 ; n ∈ N *
A. Dãy số giảm, bị chặn trên
B. Dãy số tăng, bị chặn dưới
C. Dãy số tăng, bị chặn.
D. Dãy số giảm, bị chặn dưới.
Xét tính tăng, giảm và bị chặn của các dãy số u n , biết: u n = n + 1 n
Xét tính tăng, giảm và bị chặn của dãy số ( u n ) , biết: u n = 1 1 + n + n 2
A. Dãy số tăng, bị chặn trên
B. Dãy số tăng, bị chặn dưới
C. Dãy số giảm, bị chặn
D. Cả A, B, C đều sai