a) Cách giải các phương trình lượng giác cơ bản:

+ Phương trình sin x = a.

Nếu |a| > 1 ⇒ phương trình vô nghiệm.

Nếu |a| ≤ 1 ⇒ tìm một cung α sao cho sin α = a.

Khi đó phương trình trở thành sin x = sin α

⇒ Phương trình có nghiệm: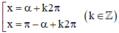 

+ Phương trình cos x = a.

Nếu |a| > 1 ⇒ phương trình vô nghiệm.

Nếu |a| ≤ 1 ⇒ tìm một cung α sao cho cos α = a.

Khi đó phương trình trở thành cos x = cos α.

⇒ Phương trình có nghiệm: x = ±α + k2π (k ∈ Z).

+ Phương trình tan x = a.

Tìm một cung α sao cho tan α = a.

Khi đó phương trình trở thành tan x = tan α.

⇒ Phương trình có nghiệm x = α + kπ (k ∈ Z).

+ Phương trình cot x = a

Tìm một cung α sao cho cot α = a.

Khi đó phương trình trở thành cot x = cot α.

⇒ Phương trình có nghiệm x = α + kπ (k ∈ Z).

b) Cách giải phương trình a.sin x + b.cos x = c.

+ Nếu a = 0 hoặc b = 0 ⇒ Phương trình lượng giác cơ bản .

+ a ≠ 0 và b ≠ 0. Chia cả hai vế của phương trình cho  ta được:

Ta giải phương trình trên như phương trình lượng giác cơ bản.

a, Điều kiện xác định: \(x \ne 90^\circ  + k180^\circ \).

Ta có:\({\rm{ }}tanx = tan55^\circ  \Leftrightarrow x = 55^\circ  + k180^\circ ,{\rm{ }}k\; \in \;\mathbb{Z}\,\,(TM).\)

b, Điều kiện xác định: \(2x + \frac{\pi }{4} \ne \frac{\pi }{2} + k\pi  \Leftrightarrow x \ne \frac{\pi }{8} + k\pi ,k \in \mathbb{Z}.\)

Ta có: \(\tan \left( {2x + \frac{\pi }{4}} \right) = 0 \Leftrightarrow 2x + \frac{\pi }{4} = k\pi  \Leftrightarrow x = -\frac{\pi }{8} + k\frac{\pi }{2},k \in \mathbb{Z}\,\,(TM).\)

Để giải phương trình cos(2x) - sin(x) = 0, ta có thể sử dụng các công thức lượng giác để đưa phương trình về dạng phù hợp.

Bước 1: Sử dụng công thức cos(2x) = 2cos^2(x) - 1, phương trình trở thành 2cos^2(x) - 1 - sin(x) = 0.

Bước 2: Sử dụng công thức sin^2(x) + cos^2(x) = 1, ta có thể thay thế cos^2(x) bằng 1 - sin^2(x), phương trình trở thành 2(1 - sin^2(x)) - 1 - sin(x) = 0.

Bước 3: Giải phương trình 2 - 2sin^2(x) - 1 - sin(x) = 0.

Bước 4: Đặt sin(x) = t, phương trình trở thành 2 - 2t^2 - 1 - t = 0.

Bước 5: Rút gọn phương trình, ta có -2t^2 - t + 1 = 0.

Bước 6: Giải phương trình bậc hai trên, ta có thể sử dụng công thức hoặc phân tích thành nhân tử để tìm giá trị của t.

Bước 7: Giải phương trình -2t^2 - t + 1 = 0, ta tìm được hai giá trị t = -1 và t = 1/2.

Bước 8: Đặt sin(x) = -1 và sin(x) = 1/2, ta tìm được hai giá trị x = -π/2 và x = π/6.

Vậy, phương trình cos(2x) - sin(x) = 0 có hai nghiệm là x = -π/2 và x = π/6.

ĐKXĐ: 1-sin x<>0

=>sin x<>1

=>x<>pi/2+k2pi

cos2x/1-sinx=0

=>cos2x=0

=>2x=pi/2+kpi

=>x=pi/2+kpi/2

Kết hợp ĐKXĐ, ta được: \(x\in\left\{pi+k2pi;\dfrac{3}{2}pi+k2pi;2pi+k2pi\right\}\)

a, Điều kiện xác định: \(\frac{1}{2}x + \frac{\pi }{4} \ne k\pi  \Leftrightarrow x \ne  - \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}.\)

Ta có: \(cot\left( {\frac{1}{2}x + \frac{\pi }{4}} \right) =  - 1 \Leftrightarrow cot\left( {\frac{1}{2}x + \frac{\pi }{4}} \right) = \cot \left( { - \frac{\pi }{4}} \right)\)

\( \Leftrightarrow \frac{1}{2}x + \frac{\pi }{4} =  - \frac{\pi }{4} + k\pi  \Leftrightarrow x =  - \pi  + k2\pi ,k \in \mathbb{Z}\,\,(TM).\)

Vậy \(x =  - \pi  + k2\pi ,k \in \mathbb{Z}\,\).

b, Điều kiện xác định: \(3x \ne k\pi  \Leftrightarrow x \ne k\frac{\pi }{3},k \in \mathbb{Z}.\)

\(\;cot3x =  - \frac{{\sqrt 3 }}{3} \Leftrightarrow cot3x = \cot \left( { - \frac{\pi }{3}} \right)\)

\( \Leftrightarrow 3x =  - \frac{\pi }{3} + k\pi  \Leftrightarrow x =  - \frac{\pi }{9} + k\frac{\pi }{3},k \in \mathbb{Z}\,\,(TM).\)

Vậy \(x =  - \frac{\pi }{9} + k\frac{\pi }{3},k \in \mathbb{Z}\,\).

\(\begin{array}{l}a)\;\,cos(x + \frac{\pi }{3}) = \frac{{\sqrt 3 }}{2}\\ \Leftrightarrow cos\left( {x + \frac{\pi }{3}} \right) = cos\frac{\pi }{6}\\ \Leftrightarrow \left[ \begin{array}{l}x + \frac{\pi }{3} = \frac{\pi }{6} + k2\pi \\x + \frac{\pi }{3} = -\frac{\pi }{6} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = -\frac{\pi }{6} + k2\pi \\x = -\frac{\pi }{2} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)

\(\begin{array}{l}b)\;\,cos4x = cos\frac{{5\pi }}{{12}}\\ \Leftrightarrow \left[ \begin{array}{l}4x = \frac{{5\pi }}{{12}} + k2\pi \\4x = -\frac{{5\pi }}{{12}} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{{5\pi }}{{48}} + k\frac{\pi }{2}\\x = -\frac{{5\pi }}{{48}} + k\frac{\pi }{2}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)

\(\begin{array}{l}c)\;\,co{s^2}x = 1\\ \Leftrightarrow \left[ \begin{array}{l}cosx = 1\\cosx = -1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = k2\pi \\x = \pi  + k2\pi \end{array} \right. \Leftrightarrow x = k\pi ,k \in \mathbb{Z}\end{array}\)

   - Thúc đẩy phát triển sản xuất và dịch vụ. Nhà nước khuyến khích các thành phần kinh tế, các nhà đầu tư trong và ngoài nước sản xuất, kinh doanh có hiệu quả nhằm tạo ra nhiều việc làm cho người lao động.

   - Khuyến khích làm giàu theo pháp luật, tự do hành nghề, khôi phục và phát triển các ngành nghề truyền thống, đẩy mạnh phong trào lập nghiệp của thanh niên.

   - Đẩy mạnh xuất khẩu lao động, đặc biệt là lao động đã qua đào tạo nghề, lao động nông nghiệp nhằm giải quyết yêu cầu trước mắt và lâu dài, tăng thu nhập cho người lao động.

   - Sử dụng có hiệu quả nguồn vốn trong chương trình mục tiêu quốc gia để giải quyết việc làm, cải thiện điều kiện làm việc cho người lao động.

a) Vì \(\sin \frac{\pi }{6} = \frac{1}{2}\) nên ta có phương trình \(sin2x = \sin \frac{\pi }{6}\)

\( \Leftrightarrow \left[ \begin{array}{l}2x = \frac{\pi }{6} + k2\pi \\2x = \pi  - \frac{\pi }{6} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{{12}} + k\pi \\x = \frac{{5\pi }}{{12}} + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)

\(\begin{array}{l}b,\,\,sin(x - \frac{\pi }{7}) = sin\frac{{2\pi }}{7}\\ \Leftrightarrow \left[ \begin{array}{l}x - \frac{\pi }{7} = \frac{{2\pi }}{7} + k2\pi \\x - \frac{\pi }{7} = \pi  - \frac{{2\pi }}{7} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{{3\pi }}{7} + k2\pi \\x = \frac{{6\pi }}{7} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)

\(\begin{array}{l}\;c)\;sin4x - cos\left( {x + \frac{\pi }{6}} \right) = 0\\ \Leftrightarrow sin4x = cos\left( {x + \frac{\pi }{6}} \right)\\ \Leftrightarrow sin4x = \sin \left( {\frac{\pi }{2} - x - \frac{\pi }{6}} \right)\\ \Leftrightarrow sin4x = \sin \left( {\frac{\pi }{3} - x} \right)\\ \Leftrightarrow \left[ \begin{array}{l}4x = \frac{\pi }{3} - x + k2\pi \\4x = \pi  - \frac{\pi }{3} + x + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{{15}} + k\frac{{2\pi }}{5}\\x = \frac{{2\pi }}{9} + k\frac{{2\pi }}{3}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)