Sử dụng phương pháp S = 2 x S - S, tìm giá trị của A = 5 + 10 + 20 + 40 +... + 1280.

Những câu hỏi liên quan
Sử dụng phương pháp S = 2S - S, tìm giá trị của 7 + 14 + 28 + .... + 896.
Sử dụng phương pháp S = 2S - S, tìm giá trị của 7+14+21+...+896.
. Giả sử ta có biến mảng A lần lượt có các giá trị của phần tử sau: a Giá trị 5 8 9 5 3 5 Chỉ số 1 2 3 4 5 6 Ta có câu lệnh S:=0; S:=S+a[1]+a[6] thì giá trị S sẽ bằng bao nhiêu: A. 8 B. 9 C. 10 D. 11
Một tam giác có S=60m vuông, độ dài cạnh đáy x và chiều cao tương ứng y có quan hệ gì
b, ứng với giá trị x là 10, 20, 30, 40, 50. tìm giá trị tương ứng của y
1. Cho x thỏa mãn x^2 - 3x + 1 = 0. Tính giá trị của S = x^2/x^4+1
2. Ko sử dụng máy tính, CMR B = 2010.2011.2016.2017 + 9 là số chính phương
gọi S là tập nghiệm của bất phương trình \(x^2-\left(2m-6\right)x+m^2-6m+5\le0\). tìm tất cả các giá trị của m sao cho (3;5) \(\subset\) S.
=>x^2-[(m-1)+(m-5)]x+m^2-6m+5<=0
=>x(x-m+1)-(m-5)(x-m+1)<=0
=>(x-m+1)(x-m+5)<=0
=>m-5<=x<=m-1
=>S=[m-5;m-1]
(3;5) là tập con của S
=>m-5>=3 và m-1<=5
=>m>=8 và m<=6
=>Loại
Đúng 0
Bình luận (0)
Biết rằng hình lập phương có sáu mặt đều là hình vuông. Giả sử x là độ dài của cạnh hình lập phương.Tính các giá trị của S ứng với các giá trị của x cho trong bảng dưới đây rồi điền vào các ô trống.
x
1/3
1/2
1
3/2
2
3
S
Đọc tiếp
Biết rằng hình lập phương có sáu mặt đều là hình vuông. Giả sử x là độ dài của cạnh hình lập phương.
Tính các giá trị của S ứng với các giá trị của x cho trong bảng dưới đây rồi điền vào các ô trống.
| x | 1/3 | 1/2 | 1 | 3/2 | 2 | 3 |
| S |
Giá trị của S và x được thể hiện trong bảng sau:
| x | 1/3 | 1/2 | 1 | 3/2 | 2 | 3 |
| S | 2/3 | 3/2 | 6 | 27/2 | 24 | 54 |
Đúng 0
Bình luận (0)
Tính diện tích S của hình thang ABCD theo x bằng hai cách: 1) Tính theo công thức: S BH x (BC + DA) : 2 2) S SABH + SBCKH + SCKD Sau đó, sử dụng giả thiết S 20 để thu được hai phương trình tương đương với nhau. Trong hai phương trình ấy, có phương trình nào là phương trình bậc nhất không?
Đọc tiếp
Tính diện tích S của hình thang ABCD theo x bằng hai cách:
1) Tính theo công thức: S = BH x (BC + DA) : 2
2) S = SABH + SBCKH + SCKD
Sau đó, sử dụng giả thiết S = 20 để thu được hai phương trình tương đương với nhau. Trong hai phương trình ấy, có phương trình nào là phương trình bậc nhất không?
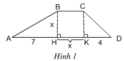
1) Ta có: S = BH x (BC + DA) : 2
+ BCKH là hình chữ nhật nên BC = KH = x
+ BH = x
+ AD = AH + HK + KD = 7 + x + 4 = 11 + x.
Vậy S = BH x (BC + DA) : 2 = x.(x + 11 + x) : 2 = x.(2x + 11) : 2.
2) S = SABH + SBCKH + SCKD
+ ABH là tam giác vuông tại H
⇒ SBAH = 1/2.BH.AH = 1/2.7.x = 7x/2.
+ BCKH là hình chữ nhật
⇒ SBCKH = x.x = x2.
+ CKD là tam giác vuông tại K
⇒ SCKD = 1/2.CK.KD = 1/2.4.x = 2x.
Do đó: S = SABH + SBCKH + SCKD = 7x/2 + x2 + 2x = x2 + 11x/2.
- Với S = 20 ta có phương trình:
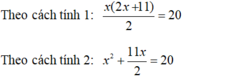
Hai phương trình trên tương đương với nhau. Và cả hai phương trình trên đều không phải là phương trình bậc nhất.
Đúng 0
Bình luận (0)
CMR : S=1+9S với S=1+2+3+4+5+6+7+8+9+10 và tìm giá trị của S
số số hạng là : `(10-1)+1:1=10`
tổng là : `(10+1) . 10 : 2=55`
`S=1+9S=>1+9.55=496`
`---------------`
cho mình hỏi đề bạn kiểu j v đọc mãi ko hiểu:)))?
Đúng 4
Bình luận (0)
Đề sai mà em up lên hoài, ko sửa đề gì hết vậy em?
Đúng 2
Bình luận (7)
Xem thêm câu trả lời


















