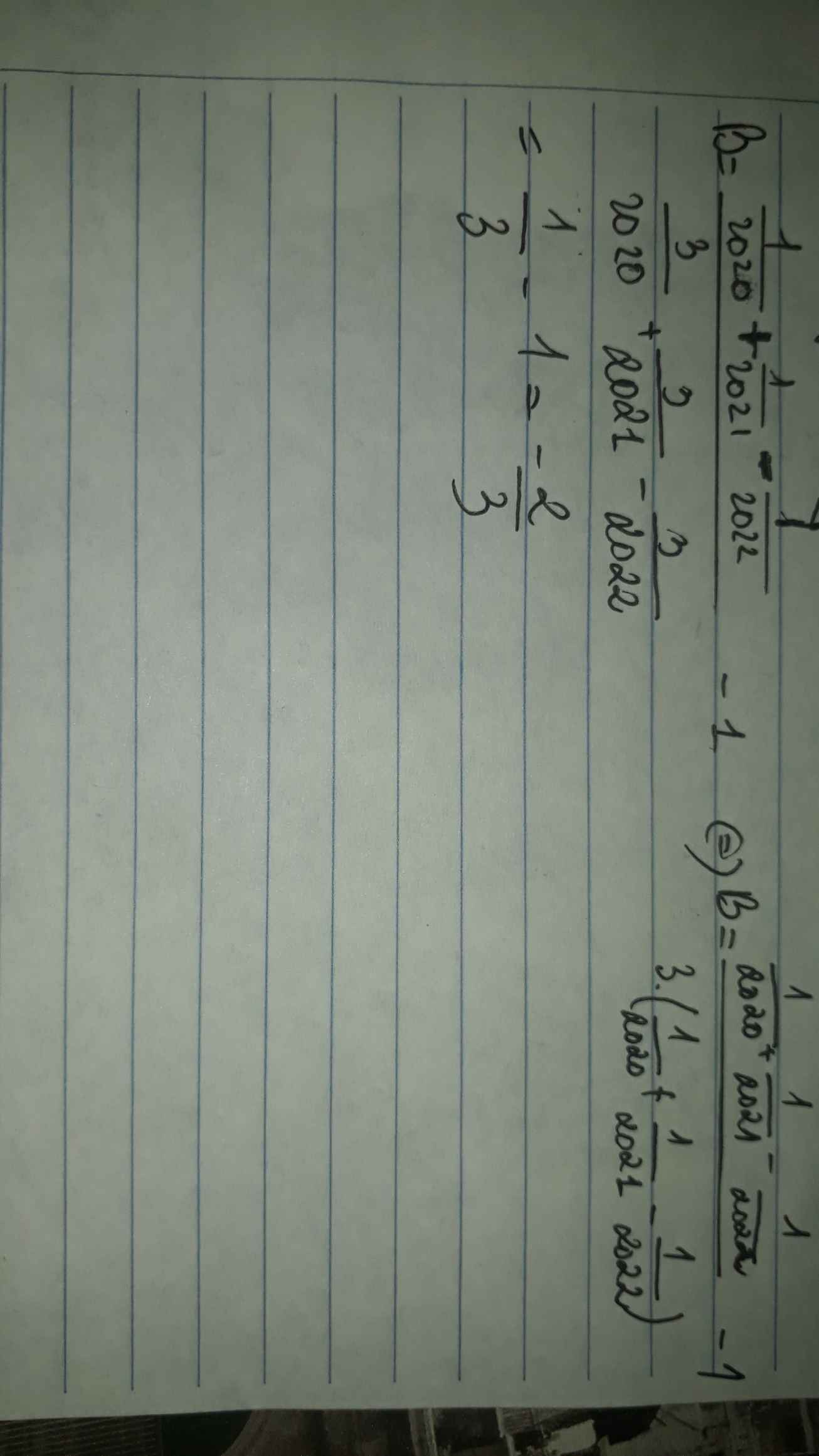2022/2021...2021/2020

Những câu hỏi liên quan
so sánh P=2019/2020+2020/2021+2021/2022 và Q=2019+2020+2021/2020+2021+2022
2020 + 2021/2021 + 2022 và 2020 + 2021 + 2022/2023
2021.(2020+2022)-2020.(2021+2022)
\(2021\left(2020+2022\right)-2020\left(2021+2022\right)\\ =2021.2020+2021.2022-2020.2021-2020.2022\\ =\left(2021.2020-2020.2021\right)+\left(2021.2022-2020.2022\right)\\ =0+2022.\left(2021-2020\right)\\ =0+2022.1=2022\)
Đúng 3
Bình luận (0)
so sanh
a)-2021/2020 va 1/2
b)2022/2021 va 2021/2020
Xem thêm câu trả lời
so sánh
\(\sqrt{2021}-\sqrt{2020}\) và \(\sqrt{2022}-\sqrt{2021}\)
\(\sqrt{2022}-\sqrt{2020}\) và \(\sqrt{2020}-\sqrt{2018}\)
Hãy so ánh tổng A với 4: 2020/2021+2021/2022+2021/2022+2023/2024
NHANH NHÉ!
Nhỏ hơn
Ta có 2020/2021 <1
2021/2022 <1
2022/2023 <1
2023/2024 <1
Suy ra A=(2021/2021+2021/2022 +2022/2023 +2023/2024) < (1+1+1+1)= 4
Vậy A <4
Chúc bạn học tốt
Đúng 1
Bình luận (0)
\(\dfrac{2020}{2021}< 1\)
\(\dfrac{2021}{2022}< 1\)
\(\dfrac{2021}{2022}< 1\)
\(\dfrac{2023}{2024}< 1\)
Do đó: A<4
Đúng 1
Bình luận (0)
Cho A = \(\dfrac{2019}{2020}\)+\(\dfrac{2020}{2021}\)+\(\dfrac{2021}{2022}\)+\(\dfrac{2022}{2019}\). Chứng tỏ A > 4
Giúp với ạ!!
Ta có:2019>4
=>2019/2020+2020/2021+2021/2022+2019>4
=>a>4(dpcm)
Đúng 1
Bình luận (0)
B=\(\dfrac{\dfrac{1}{2020}+\dfrac{1}{2021}-\dfrac{1}{2022}}{\dfrac{3}{2020}+\dfrac{3}{2021}-\dfrac{3}{2022}}-1\)
\(B=\dfrac{\dfrac{1}{2020}+\dfrac{1}{2021}-\dfrac{1}{2022}}{\dfrac{3}{2020}+\dfrac{3}{2021}-\dfrac{3}{2022}}-1=\dfrac{\dfrac{1}{2020}+\dfrac{1}{2021}-\dfrac{1}{2022}}{3\left(\dfrac{1}{2020}+\dfrac{1}{2021}-\dfrac{1}{2022}\right)}-1=\dfrac{1}{3}-1=-\dfrac{2}{3}\)
Đúng 2
Bình luận (0)
\(B=\dfrac{\dfrac{1}{2021}+\dfrac{1}{2021}-\dfrac{1}{2022}}{\dfrac{3}{2020}+\dfrac{3}{2021}-\dfrac{3}{2022}}-1=\dfrac{\dfrac{1}{2021}+\dfrac{1}{2021}-\dfrac{1}{2022}}{3\left(\dfrac{1}{2020}+\dfrac{1}{2021}-\dfrac{1}{2022}\right)}-1=\dfrac{1}{3}-1=\dfrac{1}{3}-\dfrac{3}{3}=-\dfrac{2}{3}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho \(\dfrac{x}{2020}+\dfrac{y}{2021}+\dfrac{z}{2022}=1\) và \(\dfrac{2020}{x}+\dfrac{2021}{y}+\dfrac{2022}{z}=0\) \(\left(x,y,z\ne0\right)\)
Chứng minh rằng \(\dfrac{x^2}{2020^2}+\dfrac{y^2}{2021^2}+\dfrac{z^2}{2022^2}=1\)