Cho đường tròn (O cm ;12 ) , điểm M cách O 20cm. Vẽ tiếp tuyến MA (A là tiếp điểm)
a) Tính MA.
b) Vẽ dây AB vuông góc với OM. Chứng minh MB là tiếp tuyến.
Những câu hỏi liên quan
Cho 2 đường tròn (O) và (O') tiếp xúc ngoài với nhau tại B. Vẽ đường kính AB của đường tròn (O) và đường kính BC của đường tròn (O'). Đường tròn đường kính OC cắt (O) tại M và N
a) đường thẳng CM cắt (O') tại P. CM OM // BP
b) Từ C kẻ đường thẳng vuông góc với CM cắt tia ON tại D. CM tam giác OCD là tam giác cân
a: Xét (OC/2) có
góc OMC là góc nội tiếp chắn nửa đường tròn
=>góc OMC=90 độ
=>CM vuông góc MO
Xét (O') có
góc BPC nội tiếp
BC là đường kính
=>góc BPC=90 độ
=>BP vuông góc CM
=>BP//OM
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A nội tiếp đường tròn tâm O. Đường cao AH cắt đường tròn tại D
a) Vì sao AD lad đường kính của đường tròn tâm O
b) Cho biết AC = 10 cm, BC = 12 cm. Tính đường cao AH và BK của đường tròn tâm O
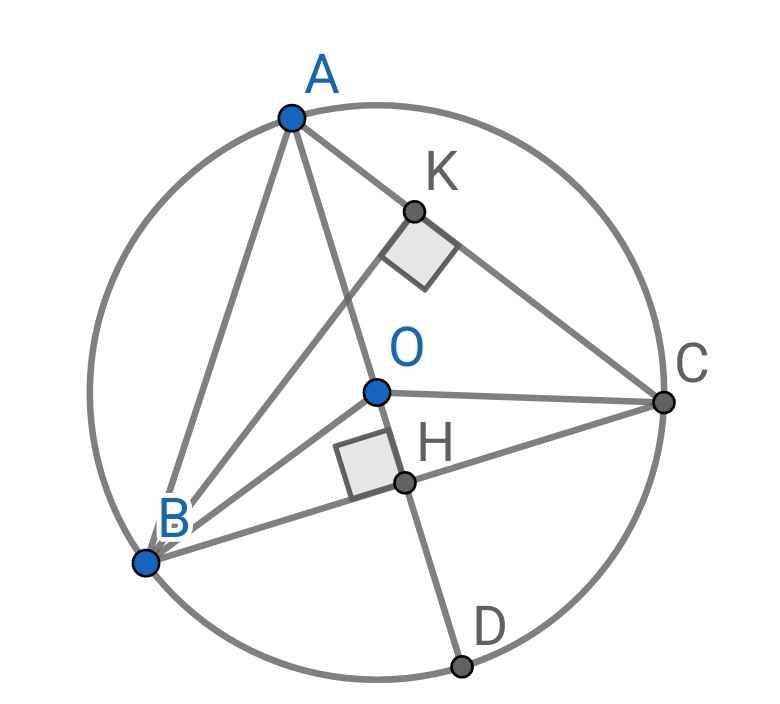a) Ta có:
OB = OC (bán kính)
⇒ O nằm trên đường trung trực của BC (1)
Do ∆ABC cân tại A (gt)
AH là đường cao (gt)
⇒ AH cũng là đường trung trực của ∆ABC
⇒ AH là đường trung trực của BC (2)
Từ (1) và (2) suy ra O ∈ AH
⇒ O ∈ AD
Vậy AD là đường kính của (O)
b) Sửa đề: Tính độ dài các đường cao AH, BK của ∆ABC
Do AH là đường trung trực của BC (cmt)
⇒ H là trung điểm của BC
⇒ CH = BC : 2
= 12 : 2
= 6 (cm)
∆AHC vuông tại H
⇒ AC² = AH² + CH² (Pytago)
⇒ AH² = AC² - CH²
= 10² - 6²
= 64
⇒ AH = 8 (cm)
⇒ sinACH = AH/AC
= 4/5
⇒ ACH ≈ 53⁰
⇒ BCK ≈ 53⁰
∆BCK vuông tại K
⇒ sinBCK = BK/BC
⇒ BK = BC.sinBCK
= 10.sin53⁰
≈ 8 (cm)
Đúng 4
Bình luận (0)
. Cho đường tròn(O) đường kính BC, lấy điểm A trên đường tròn sao cho AB<AC
a. Cm:ABC vuông
b. Kẻ tiếp tuyến Cx với đường tròn, gọi I là trung điểm của AC, OI cắt Cx tại M Cm: MA là tiếp tuyến của đường tròn (O)
c. MB cắt đường tròn (O) tại K. Cm: CI.CO=CK.CB
a: Xét (O) có
ΔABC nội tiếp
BC là đường kính
Do đó: ΔABC vuông tại A
Đúng 0
Bình luận (0)
. Cho đường tròn(O) đường kính BC, lấy điểm A trên đường tròn sao cho AB<AC
a. Cm:ABC vuông
b. Kẻ tiếp tuyến Cx với đường tròn, gọi I là trung điểm của AC, OI cắt Cx tại M Cm: MA là tiếp tuyến của đường tròn (O)
c. MB cắt đường tròn (O) tại K. Cm: CI.CO=CK.CB
a, Vì \(\widehat{BAC}=90^0\) (góc nt chắn nửa đg tròn) nên tg ABC vuông tại A
Đúng 0
Bình luận (1)
Cho hai đường tròn (O; 13 cm), (O’; 5 cm) và OO' = 8 cm. Vị trí tương đối của hai đường tròn đó là:
Cho đường tròn (O) đường kính AB = 10 cm C là điểm trên đường tròn (O) sao cho AC = 8 cm. Vẽ CH ⊥ AB (H ∈ AB)
c) Tiếp tuyến tại A của đường tròn (O) cắt BC tại E. Chứng minh:CE.CB = AH. AB
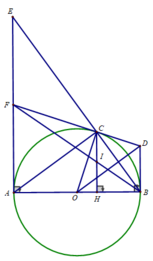
c) Xét tam giác ACB vuông tại C, CH là đường cao nên :
AH.AB = A C 2
Xét tam giác ABE vuông tại A, AC là đường cao nên :
EC.BC = A C 2
⇒ AH.AB = EC.BC
Đúng 0
Bình luận (0)
Cho đường tròn tâm O từ điểm A nằm ngoài đường tròn vẽ 2 tiếp tuyến tới đường tròn AM,AN(MN là 2 tiếp điểm a) CM 4 điểm A,M,O,N thuộc cùng 1 đường tròn b) vẽ đường kính MOB.tia phân giác góc NOB cắt AN tại i CM IB là tiếp tuyến đường tròn O c) CM AO là đường trung trực của MN gọi K là giao điểm của AO và MN CM k là trng điểm của MN.
a: Xét tứ giác OMAN có
\(\widehat{OMA}+\widehat{ONA}=90^0+90^0=180^0\)
=>OMAN là tứ giác nội tiếp
=>O,M,A,N cùng thuộc một đường tròn
b: ΔOBN cân tại O
mà OI là đường phân giác
nên OI\(\perp\)BN và OI là đường trung trực của BN
Xét ΔOBI và ΔONI có
OB=ON
\(\widehat{BOI}=\widehat{NOI}\)
OI chung
Do đó: ΔOBI=ΔONI
=>\(\widehat{OBI}=\widehat{ONI}=90^0\)
=>IB là tiếp tuyến của (O)
c: Xét (O) có
AM,AN là tiếp tuyến
=>AM=AN
=>A nằm trên đường trung trực của MN(1)
OM=ON
=>O nằm trên đường trung trực của MN(2)
Từ (1) và (2) suy ra AO là đường trung trực của MN
d: AO là đường trung trực của MN
=>AO cắt MN tại trung điểm của MN
=>K là trung điểm của MN
Đúng 2
Bình luận (0)
Cho đường tròn (O) đường kính AB = 10 cm C là điểm trên đường tròn (O) sao cho AC = 8 cm. Vẽ CH ⊥ AB (H ∈ AB)
b) Tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại D. Chứng minh OD ⊥ BC
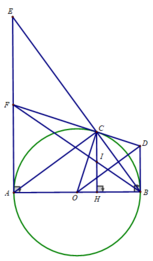
b) DC và DB là 2 tiếp tuyến cắt nhau tại D
⇒ DC = DB
Lại có: OC = OB = R
⇒ OD là đường trung trực của BC hay OD ⊥ BC
Đúng 0
Bình luận (0)
Cho đường tròn (O; 5 cm) và điểm A sao cho OA = 5 cm. Đường thẳng xy đi qua điểm A. Chứng minh đường thẳng xy và đường tròn (O; 5 cm) có ít nhất một điểm chung
Kẻ OH vuông góc với xy suy ra OH ≤ OA. Mặt khác A nằm trong đường tròn (O;R) nên OA=R => đpcm
Đúng 0
Bình luận (0)
cho nữa đường tròn (O) đường kính AB=2R. Vẽ đường tròn tâm K đường kinh OB.
a..CM hai đường tròn tâm O và K tiếp xúc nhau
b..vẽ dây BD khác đường kinh của đường tròn (O) nó cắt đường tròn(K) tại M. CM KM//OD