Do d qua K nên pt d có dạng: \(y=kx-k+3\) (với \(k\ne0;3\))

Gọi A và B lần lượt là giao điểm của d với Ox; Oy

\(\Rightarrow\left\{{}\begin{matrix}A\left(\dfrac{k-3}{k};0\right)\\B\left(0;-k+3\right)\end{matrix}\right.\)

Để A; B có hoành độ dương (do nằm trên các tia Ox; Oy) \(\Rightarrow k< 0\)

Khi đó: \(OA=\dfrac{k-3}{k}\) ; \(OB=-k+3\)

\(S_{OAB}=\dfrac{1}{2}OA.OB=6\Leftrightarrow\dfrac{\left(k-3\right)\left(-k+3\right)}{k}=12\)

\(\Leftrightarrow k^2+6k+9=0\Leftrightarrow k=-3\)

Phương trình d: \(y=-3x+6\)

Thay x=4 vào (P), ta được:

y=1/2*4^2=8

1.

\(\left(C\right):x^2+y^2-2x-4=0\)

\(\Leftrightarrow\left(x-1\right)^2+y^2=5\)

Đường tròn \(\left(C\right)\) có tâm \(I=\left(1;0\right)\), bán kính \(R=\sqrt{5}\)

Phương trình đường thẳng \(d_1\) có dạng: \(x+y+m=0\left(m\in R\right)\)

Mà \(d_1\) tiếp xúc với \(\left(C\right)\Rightarrow d\left(I;d_1\right)=\dfrac{\left|1+m\right|}{\sqrt{2}}=\sqrt{5}\)

\(\Leftrightarrow\left|m+1\right|=\sqrt{10}\)

\(\Leftrightarrow m=-1\pm\sqrt{10}\)

\(\Rightarrow\left[{}\begin{matrix}d_1:x+y-1+\sqrt{10}=0\\d_1:x+y-1-\sqrt{10}=0\end{matrix}\right.\)

2.

Phương trình đường thẳng \(\Delta\) có dạng: \(x-y+m=0\left(m\in R\right)\)

Ta có: \(d\left(I;\Delta\right)=\sqrt{R^2-\dfrac{MN^2}{4}}=2\)

\(\Leftrightarrow\dfrac{\left|m+1\right|}{\sqrt{2}}=2\)

\(\Leftrightarrow m=-1\pm2\sqrt{2}\)

\(\Rightarrow\left[{}\begin{matrix}\Delta:x-y+1+2\sqrt{2}=0\\\Delta:x-y+1-2\sqrt{2}=0\end{matrix}\right.\)

3.

Vì \(P\in d\Rightarrow P=\left(m;m+1\right)\left(m\in R\right)\)

\(\Rightarrow IP=\sqrt{\left(m-1\right)^2+\left(m+1\right)^2}=\sqrt{2m^2+2}\)

Ta có: \(cosAIP=cos60^o=\dfrac{R}{IP}=\dfrac{\sqrt{5}}{IP}=\dfrac{1}{2}\Rightarrow IP=2\sqrt{5}\)

\(\Rightarrow\sqrt{2m^2+2}=2\sqrt{5}\)

\(\Leftrightarrow2m^2+2=20\)

\(\Leftrightarrow m=\pm3\)

\(\Rightarrow\left[{}\begin{matrix}P=\left(3;4\right)\\P=\left(-3;-2\right)\end{matrix}\right.\)

Cắt trục hoành thì cái điểm đó tung độ sẽ bằng 0 chứ sao có thể là -2

Em sửa lại đề:

Hoặc là d2 cắt trục tung

Hoặc là hoành độ là -2

1) Xác định được ít nhất hai điểm phân biệt thuộc đường thẳng d.  Chẳng hạn:  A ( − 3 ; 0 ) ;   B ( 0 ; 3 ) .

Xác định được đỉnh và ít nhất hai điểm thuộc (P) . Chẳng hạn :  O ( 0 ; 0 ) ;   C ( 6 ; 9 ) ;   E ( − 6 ; 9 ) .

Đồ thị

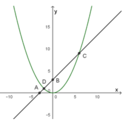
2) Phương trình hoành độ giao điểm:  1 4 x 2 = x + 3 ⇔ 1 4 x 2 − x − 3 = 0 ⇔ x = − 2  hoặc x= 6

Tọa độ giao điểm là  D ( − 2 ; 1 )   v à   C ( 6 ; 9 ) .  

\(a,\) \(\left(d\right)\) cắt Ox tại A nên \(x=0\Rightarrow y=2\cdot0-2=-2\Rightarrow A\left(0;-2\right)\)

\(\left(d\right)\) cắt Oy tại B nên \(y=0\Rightarrow2x-2=0\Rightarrow x=1\Rightarrow B\left(1;0\right)\)

Từ đó ta được \(OA=2;OB=1\)

Gọi H là chân đường vuông góc từ O đến \(\left(d\right)\)

Áp dụng HTL:

\(\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}=\dfrac{1}{2}+\dfrac{1}{1}\\ \Rightarrow\dfrac{1}{OH^2}=\dfrac{3}{2}\Rightarrow OH^2=\dfrac{3}{2}\Rightarrow OH=\dfrac{\sqrt{6}}{2}\)

\(b,S_{AOB}=\dfrac{1}{2}OA\cdot OB=\dfrac{1}{2}\cdot1\cdot2=1\left(đvdt\right)\)