cho đoạn AB=35cm,trên cùng một nửa mặt phẳng bờ AB vẽ các đoạn thẳng AC,BD cùng vuông góc với AB và AC=5cm,BD =17cm.Tính CD?

Những câu hỏi liên quan
cho đoạn AB=35cm, Trên cùng nửa mặt phẳng bờ AB vẽ các đoạn thẳng AC,BD cùng vuông góc với AB vá AC=5cm,BD=17cm . tính CD?
Cho đoạn thẳng AB, O là trung điểm AB. Trên cùng một nửa mặt phẳng bờ AB vẽ các tia Ax; By vuông góc với AB. Gọi C là một điểm thuộc D. Tính DC biết AC=5cm;BD=2cm
A. CD=7cm
B. CD=3cm
C. CD=5cm
D. CD=2cm
Câu 26: Cho đoạn thẳng AB, O là trung điểm AB. Trên cùng một nửa mặt phẳng bờ AB vẽ các tia Ax; By vuông góc với AB. Gọi C là một điểm thuộc D. Tính DC biết AC = 5cm; BD = 2cm
A. CD = 7 cm B. CD = 3 cm C. CD = 5 cm D. CD = 2 cm
vẽ đoạn thẳng BC.Trên cùng 1 nửa mặt phẳng bờ AB vẽ 2 tia Ax và By cùng vuông góc với AB . Gọi O là trung điểm của AB. trên Ax và By lấy các điểm lần lượt C và D sao cho góc COD = 90o .
CMR a, AC + BD = CD
b, AC x BC = \(\dfrac{AB^2}{4}\)
Cho đoạn AB, trên hai nửa mặt phẳng đối nhau bờ AB vẽ các đoạn thẳng AC, BD sao cho AC = BD và AC vuông góc với AB, BD vuông góc với AB. Gọi M là trung điểm của AB. CMR : C, M, D thẳng hằng
Xét ΔAMC vuông tại A và ΔBMD vuông tại B có
MA=MB(M là trung điểm của AB)
AC=BD(gt)
Do đó: ΔAMC=ΔBMD(hai cạnh góc vuông)
nên \(\widehat{AMC}=\widehat{BMD}\)(hai góc tương ứng)
mà \(\widehat{AMC}+\widehat{BMC}=180^0\)(hai góc kề bù)
nên \(\widehat{BMD}+\widehat{BMC}=180^0\)
\(\Leftrightarrow\widehat{CMD}=180^0\)
hay C,M,D thẳng hàng(đpcm)
Đúng 1
Bình luận (0)
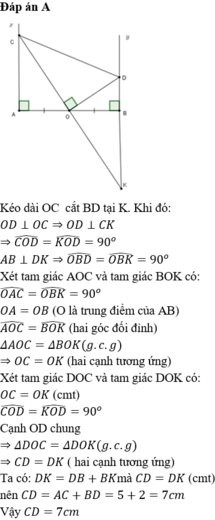
Cho đoạn thẳng AB, O là trung điểm AB. Trên cùng 1 nửa mặt phẳng bờ AB, vẽ các tia Ax và By vuông góc với AB. Gọi C là 1 điểm thuộc tia Ax. Đường vuông góc với OC cắt By tại D. CMR CD = AC + BD
Gọi K là giao điểm của CO và BD
Xét \(\Delta\)AOC và \(\Delta\)BOK có :
AO = BO(gt)
\(\widehat{OAC}=\widehat{OBK}\left(=90^0\right)\)
\(\widehat{O}\)chung
=> \(\Delta\)AOC = \(\Delta\)BOK(g.c.g)
=> OC = OK(hai cạnh tương ứng)
AC = BK(hai cạnh tương ứng)
Xét \(\Delta\)COD và \(\Delta\)KOD có :
CO = KO(gt)
\(\widehat{OCD}=\widehat{OKD}\left(=90^0\right)\)
OD cạnh chung
=> \(\Delta\)COD = \(\Delta\)KOD(c.g.c)
=> CD = KD(hai cạnh tương ứng)
Do đó : CD = DB + BK = DB + AC
Cho đoạn thẳng AB, O là trung điểm của AB. Trên cùng một nửa mặt phẳng bờ AB, vẽ các tia Ax, By vuông góc với AB. Gọi C là một điểm thuộc tia Ax. Đường thẳng vuông góc với OC tại O cắt tia By ở D. C/m CD=AC+BD
Bài 6: Cho đoạn thẳng AB. Trên cùng một nửa mặt phẳng bờ AB vẽ các tia Ax, By cùng
vuông góc với AB. Gọi O là trung điểm của AB. Trên tia Ax lấy điểm C, trên tia By lấy
điểm D sao cho OC vuông góc OD.
a) Chứng minh AC + BD = CD.
b) Hạ OM vuông góc với CD tại M. Gọi giao điểm của AD và BC là N.
Chứng minh MN // AC.
gấp ạ
Cho đoạn thẳng AB, O là trung điểm của AB. Trên cùng một nửa mặt phẳng bờ AB, vẽ các tia Ax và By vuông góc với AB. Gọi C là một điểm thuộc tia Ax. Đường vuông góc với OC tại O cắt tia By ở D. Chứng minh rằng CD = AC + BD.
CM tg OAC đồng dạng tg OBD ( g - g )
=> OA.OB = AC.BD
mà OA = OB
=> OA\(^2\)= AC.BD
tg OAC vuông tại A có :
OC2 = AC\(^2\)+ OA2
tg OBD vuông tại B có :
OD2 = BD2 + OB2
tg OBD vuông tại O có :
CD2 = OC2 + OD2 = AC\(^2\)+ OA2 + BD2 + OB2 = AC2 + 2OA2 + BD2
= AC2 + 2AC.BD + BD2
= ( AC + BD ) 2
=> CD = AC + BD
CHO TICK NHA !
Đúng 0
Bình luận (0)