Bài làm

x⁴ - 2x² - 144x - 1295 = 0

<=> x⁴ + 2x² - 4x² - 144x - 1296 + 1 = 0

<=> ( x⁴ + 2x² + 1 ) - ( 4x² + 144x + 1296 ) = 0

<=> ( x² + 1 )² - ( 2x + 36 )² = 0

<=> ( x² + 1 - 2x - 36 )( x² + 1 + 2x + 36 ) = 0

<=> ( x² - 2x - 35 )( x² + 2x + 37 ) = 0

<=> ( x² + 5x - 7x - 35 ) ( x² + 2x + 1 + 36 ) = 0

<=> [ x( x + 5 ) - 7( x + 5 ) ][ ( x² + 2x + 1 ) + 36 ] = 0

<=> ( x + 5 )( x - 7 )[ ( x + 1 )² + 36 ] = 0

Ta có: ( x + 1 )² \(\ge\)0

<=> ( x + 1 )² + 36 \(\ge\)36

=> ( x + 5 )( x - 7 ) = 0

<=> \(\left[{}\begin{matrix}x+5=0\\x-7=0\end{matrix}\right.\)

<=> \(\left[{}\begin{matrix}x=-5\\x=7\end{matrix}\right.\)

Vậy tập nghiệm phương trình trên là: S = { -5; 7 }

# Học tốt #

Bài này không nhất thiết phải đặt ẩn phụ nên mình giải luôn nhé.

\(x^4-2x^2-144x-1295=0\\ \Leftrightarrow x^4-4x^2+2x^2-144x+1-1296=0\\\Leftrightarrow \left(x^4+2x^2+1\right)-\left(4x^2+144x+1296\right)=0\\ \Leftrightarrow\left(x^2+1\right)^2-\left(2x+36\right)=0\\ \Leftrightarrow\left(x^2+1-2x-36\right)\left(x^2+1+2x+36\right)=0\\ \Leftrightarrow\left(x^2-2x-35\right)\left[\left(x+1\right)^2+36\right]=0\\\Leftrightarrow \left(x^2+5x-7x-35\right)\left[\left(x+1\right)^2+36\right]=0\\ \Rightarrow\left(x+5\right)\left(x-7\right)\left[\left(x+1\right)^2+36\right]=0\\ \Leftrightarrow\left[{}\begin{matrix}x+5=0\\x-7=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-5\\x=7\end{matrix}\right.\left(vi\left[\left(x+1\right)^2+36>0\forall\right]x\right)\)

Vậy tập nghiệm của phương trình trên là \(S=\left\{-5;7\right\}\)

$x^4-2x^2-144x-1295=0$

$\iff \left(x^4+2x^2+1\right)-\left(4x^2+144x+1296\right)=0$

$\iff {\left(x^2+1\right)}^2-{\left(2x+36\right)}^2=0$

$\iff \left(x^2+1+2x+36\right)\left[x^2+1-\left(2x+36\right)\right]=0$

$\iff \left(x^2+2x+37\right)\left(x^2-2x-35\right)=0$

$\iff \left(x^2+5x-7x-35\right)\left(x^2+2x+1+36\right)=0$

$\iff \left[x\left(x+5\right)-7\left(x+5\right)\right]\left[{\left(x+1\right)}^2+36\right]=0$

$\iff \left(x+5\right)\left(x-7\right)\left[{\left(x+1\right)}^2+36\right]=0$

Dễ thấy:${\left(x+1\right)}^2+36\ge 36>0\forall x$ (vô nghiệm)

$\Rightarrow [\begin{array}{c}x+5=0\\ x-7=0\end{array}$$\Rightarrow [\begin{array}{c}x=-5\\ x=7\end{array}$

x + 1 x 2 - 4 . x + 1 x + 3 = 0   Đ ặ t   t = x + 1 x

(1) trở thành: t2 – 4t + 3 = 0 (2)

Giải (2):

Có a = 1; b = -4; c = 3

⇒ a + b + c = 0

⇒ (2) có nghiệm t1 = 1; t2 = c/a = 3.

+ t = 1 ⇒ x + 1/x = 1 ⇔ x2 + 1 = x ⇔ x2 – x + 1 = 0

Có a = 1; b = -1; c = 1 ⇒ Δ = (-1)2 – 4.1.1 = -3 < 0

Phương trình vô nghiệm.

 a)  2 x 2 − 2 x 2 + 3 x 2 − 2 x + 1 = 0 ( 1 )

Đặt  x 2   –   2 x   =   t ,

(1) trở thành :   2 t 2   +   3 t   +   1   =   0   ( 2 ) .

Giải (2) :

Có a = 2 ; b = 3 ; c = 1

⇒ a – b + c = 0

⇒ (2) có nghiệm    t 1   =   - 1 ;   t 2   =   - c / a   =   - 1 / 2 .

+ Với t = -1  ⇒ x 2 − 2 x = − 1 ⇔ x 2 − 2 x + 1 = 0 ⇔ ( x − 1 ) 2 = 0 ⇔ x = 1

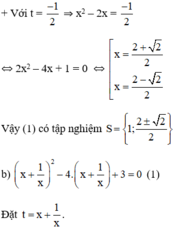
(1) trở thành:  t 2   –   4 t   +   3   =   0   ( 2 )

Giải (2):

Có a = 1; b = -4; c = 3

⇒ a + b + c = 0

⇒ (2) có nghiệm  t 1   =   1 ;   t 2   =   c / a   =   3 .

+ t = 1 ⇒ x + 1/x = 1  ⇔   x 2   +   1   =   x   ⇔   x 2   –   x   +   1   =   0

Có a = 1; b = -1; c = 1  ⇒   Δ   =   ( - 1 ) 2   –   4 . 1 . 1   =   - 3   <   0

Phương trình vô nghiệm.

ĐKXĐ: \(x\ge1\)

Do \(\sqrt{x-\sqrt{x^2-1}}.\sqrt{x+\sqrt{x^2-1}}=\sqrt{x^2-x^2+1}=1\)

Đặt \(\sqrt{x-\sqrt{x^2-1}}=t\Rightarrow\sqrt{x+\sqrt{x^2-1}}=\dfrac{1}{t}\)

Phương trình trở thành:

\(t+\dfrac{1}{t}=2\Rightarrow t^2-2t+1=0\Rightarrow t=1\)

\(\Rightarrow\sqrt{x-\sqrt{x^2-1}}=1\Leftrightarrow x-\sqrt{x^2-1}=1\)

\(\Leftrightarrow x-1=\sqrt{x^2-1}\)

\(\Rightarrow x^2-2x+1=x^2-1\)

\(\Rightarrow x=1\) (thỏa mãn)

\(\sqrt{x^2-x+1}+\sqrt{x^2-9x+9}=2x\)

=>\(\sqrt{x^2-x+1}-x+\sqrt{x^2-9x+9}-x=0\)

=>\(\dfrac{x^2-x+1-x^2}{\sqrt{x^2-x+1}+x}+\dfrac{x^2-9x+9-x^2}{\sqrt{x^2-9x+9}+x}=0\)

=>\(\left(-x+1\right)\left(\dfrac{1}{\sqrt{x^2-x+1}+x}+\dfrac{9}{\sqrt{x^2-9x+9}+x}\right)=0\)

=>-x+1=0

=>x=1

Đặt m = x - 1 .Điều kiện : m ≥ 0, x  ≥  1

Ta có : x -  x - 1 -3 = 0 ⇔ (x -1) - x - 1  -2 =0

⇔  m 2  -m - 2 =0

Phương trình  m 2  -m - 2 = 0 có hệ số a = 1, b = -1 , c = -2 nên có dạng

a – b + c = 0

Suy ra :  m 1  = -1 (loại) ,  m 2  = -(-2)/1 = 2

Với m =2 ta có: x - 1  =2 ⇒ x -1 =4 ⇔ x =5

Giá trị của x thỏa mãn điều kiện bài toán

Vậy phương trình đã cho có 1 nghiệm : x=5