Tìm nghiệm nguyên của phương trình:

Những câu hỏi liên quan
tìm nghiệm nguyên của phương trình 2xy + 4x + 2y + 1 > 5x2 + 2y2
\(\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(4x^2-4x+1\right)+\left(y^2-2y+1\right)< 3\)
\(\Leftrightarrow\left(x-y\right)^2+\left(2x-1\right)^2+\left(y-1\right)^2< 3\)
\(\Rightarrow\left(2x-1\right)^2< 3\) (1)
\(\Rightarrow\left(2x-1\right)^2=\left\{0;1\right\}\)
\(\Rightarrow\left[{}\begin{matrix}2x-1=0\\2x-1=1\\2x-1=-1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
- Với \(x=0\Rightarrow2y^2-2y< 1\Rightarrow\left(2y-1\right)^2< 3\Rightarrow\left[{}\begin{matrix}y=0\\y=1\end{matrix}\right.\) (giải như (1))
- Với \(x=1\Rightarrow2y^2+5< 4y+5\Rightarrow y^2-2y< 0\)
\(\Rightarrow y\left(y-2\right)< 0\Rightarrow0< y< 2\Rightarrow y=1\)
Vậy \(\left(x;y\right)=\left(0;0\right);\left(0;1\right);\left(1;1\right)\)
Đúng 1
Bình luận (0)
Tìm nghiệm nguyên của phương trình 2xy + 4x + 2y + 1 > 5x2 + 2y2 . Giúp mình với ạ. Mình cần gấp
1) Tìm nghiệm nguyên của phương trình : x2= 2y2+2013
2) Giải phương trình x3+2x2- 4x +\(\dfrac{8}{3}\)=0
Ta có \(2y^2⋮2\Rightarrow x^2\equiv1\left(mod2\right)\Rightarrow x^2\equiv1\left(mod4\right)\Rightarrow2y^2⋮4\Rightarrow y⋮2\Rightarrow x^2\equiv5\left(mod8\right)\) (vô lí).
Vậy pt vô nghiệm nguyên.
Đúng 0
Bình luận (0)
2: \(PT\Leftrightarrow3x^3+6x^2-12x+8=0\Leftrightarrow4x^3=\left(x-2\right)^3\Leftrightarrow\sqrt[3]{4}x=x-2\Leftrightarrow x=\dfrac{-2}{\sqrt[3]{4}-1}\).
Đúng 0
Bình luận (0)
Giải phương trình nghiệm nguyên : x2 + 2y2 + 3xy - x = 2
Lời giải:
PT $\Leftrightarrow x^2+x(3y-1)+(2y^2-2)=0$
Coi đây là pt bậc 2 ẩn $x$ thì:
$\Delta=(3y-1)^2-4(2y^2-2)=y^2-6y+9=(y-3)^2$. Do đó pt có 2 nghiệm:
$x_1=\frac{1-3y+y-3}{2}=-y-1$
$x_2=\frac{1-3y+3-y}{2}=2-2y$
Đến đây bạn thay vô pt ban đầu để giải pt bậc 2 một ẩn thui.
Đúng 2
Bình luận (0)
Bài 1 : tìm x ; y nguyên dương
2xy + x + y = 83
Bài 2 tìm nghiệm nguyên của phương trình :
a ) x2 + 2y2 + 3xy - x - y + 3 = 0
b ) 6x2y3 + 3x2 - 10y3 = -2
Cho phương trình 2 y 2 − 3 y + 7 − m = − 2 y 2 + 6 − y 3 . Tìm giá trị của tham số m để phương trình nhận y=-3 là nghiệm.
Tìm tất cả các nghiệm nguyên của phương trình x5-2x4+2x2-(y2+3)x+2y2-2=0
\(x^5\) - 2\(x^4\) - (y2 + 3)\(x\) + 2y2 - 2 = 0
(\(x^5\) - 2\(x^4\))- (y2 + 3)\(x\) + 2.(y2 + 3) - 8 = 0
\(x^4\).(\(x\) - 2) - (y2 + 3).(\(x\) - 2) - 8 = 0
(\(x\) - 2).(\(x^4\) - y2 - 3) = 8
8 = 23; Ư(8) = {-8; - 4; -2; - 1; 1; 2; 4; 8}
Lập bảng ta có:
| \(x-2\) | -8 | -4 | -2 | -1 | 1 | 2 | 4 | 8 |
| \(x\) | -6 | -2 | 0 | 1 | 3 | 4 | 6 | 10 |
| \(x^4\) - y2 - 3 | -1 | -2 | -4 | -8 | 8 | 4 | 2 | 1 |
| y | \(\pm\)\(\sqrt{1294}\) | \(\pm\)\(15\) | \(\pm\)1 | \(\pm\)\(\sqrt{6}\) | y2 = -10 (ktm) | \(\pm\)\(\sqrt{249}\) | \(\pm\)\(\sqrt{1291}\) | \(\pm\)\(\sqrt{9996}\) |
vì \(x\); y nguyên nên theo bảng trên ta có các cặp \(x\); y thỏa mãn đề bài là:
(\(x\); y) = (0; -1;); (0; 1)
Đúng 0
Bình luận (0)
Cho hệ phương trình
x
2
+
2
y
2
8
2
x
+
y
m...
Đọc tiếp
Cho hệ phương trình x 2 + 2 y 2 = 8 2 x + y = m Giá trị lớn nhất của m để hệ phương trình có nghiệm là:
A. m = 8
B. m = 2
C. m = 4
D. m = 6
Đáp án: D
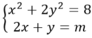
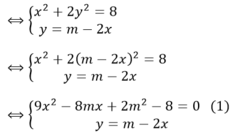
Để hệ phương trình có nghiệm thì phương trình (1) có nghiệm, tức là:
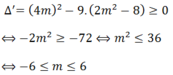
Vậy giá trị lớn nhất của m để hệ phương trình có nghiệm là 6.
Đúng 0
Bình luận (0)
Bài 12: Tìm nghiệm của các đa thức sau:a/ A(x) 2x2 - 4x b/ B(y) 3y3 + 4y - 2y2 - 3y3 - 5 + 2y2 - 3c/ C(t) 3t2 - 5 + t - 1 – t d/ M(x) 5x2 - 4 - 3x2 + 2x + 5 - 2x e/ N(x) 2x2 - 8
Đọc tiếp
Bài 12: Tìm nghiệm của các đa thức sau:
a/ A(x) = 2x2 - 4x b/ B(y) = 3y3 + 4y - 2y2 - 3y3 - 5 + 2y2 - 3
c/ C(t) = 3t2 - 5 + t - 1 – t d/ M(x) = 5x2 - 4 - 3x2 + 2x + 5 - 2x e/ N(x) = 2x2 - 8
a) cho A(x) = 0
\(=>2x^2-4x=0\)
\(x\left(2-4x\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\4x=2\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{2}\end{matrix}\right.\)
b)\(B\left(y\right)=4y-8\)
cho B(y) = 0
\(4y-8=0\Rightarrow4y=8\Rightarrow y=2\)
c)\(C\left(t\right)=3t^2-6\)
cho C(t) = 0
\(=>3t^2-6=0=>3t^2=6=>t^2=2\left[{}\begin{matrix}t=\sqrt{2}\\t=-\sqrt{2}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
d)\(M\left(x\right)=2x^2+1\)
cho M(x) = 0
\(2x^2+1=0\Rightarrow2x^2=-1\Rightarrow x^2=-\dfrac{1}{2}\left(vl\right)\)
vậy M(x) vô nghiệm
e) cho N(x) = 0
\(2x^2-8=0\)
\(2\left(x^2-4\right)=0\)
\(2\left(x^2+2x-2x-4\right)=0\)
\(2\left(x-2\right)\left(x+2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-2=0\\x+2=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
Đúng 1
Bình luận (0)
`e, N(x) = 2x^2 - 8 = 2( x^2 - 4 ) = 2( x-2 )( x + 2 )`
Xét `N(x)=0`
`=> 2(x-2)(x+2)=0`
`=>(x-2)(x+2)=0`
`=>x-2=0` hoặc `x+2=0`
`=>x=2` hoặc `x=-2`
Vậy `x in { +-2 }` là nghiệm của `N(x)`
Đúng 1
Bình luận (0)
Xem thêm câu trả lời


















