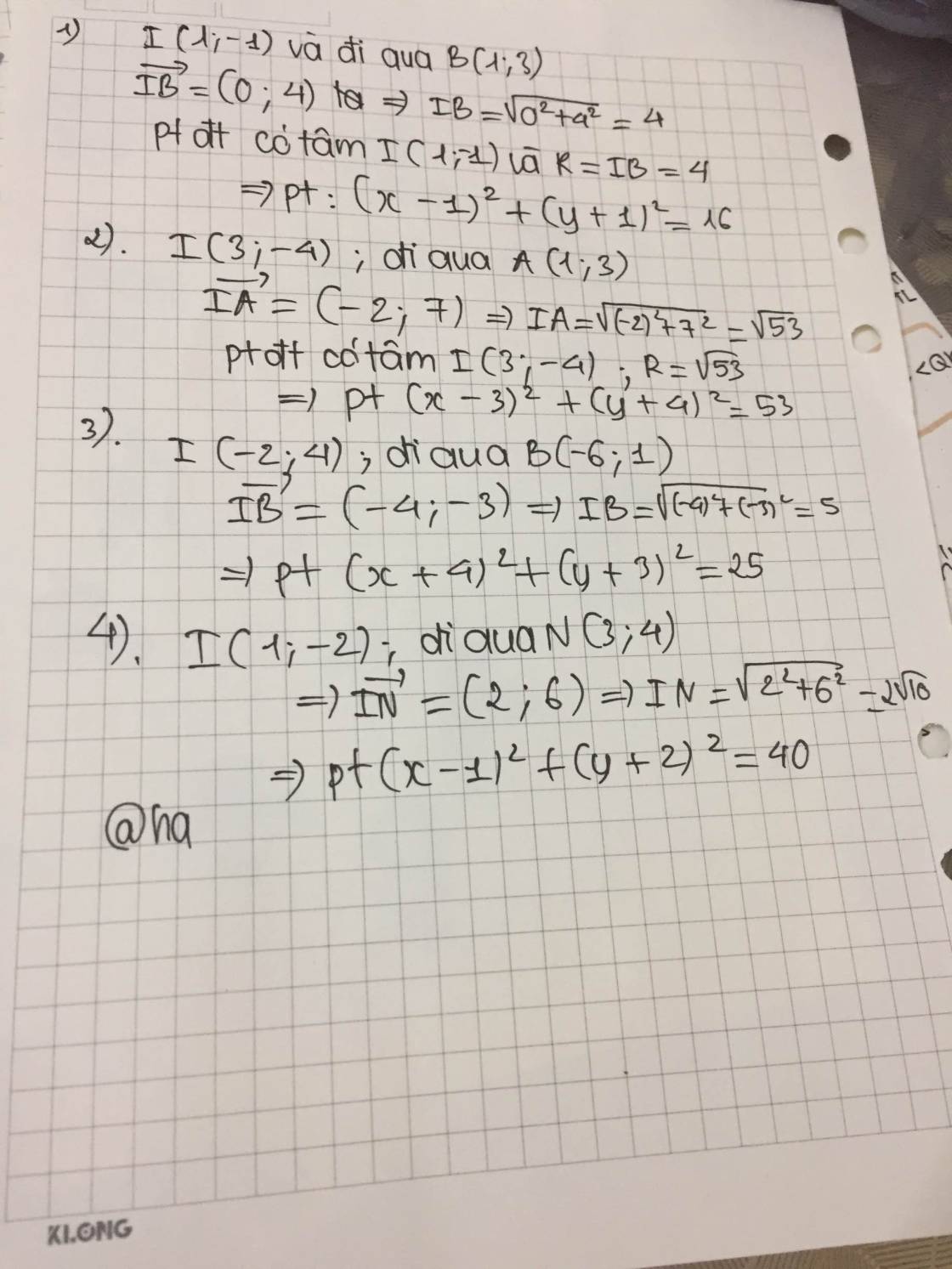. Đường tròn đi qua điểm M(-3;-4) và có tâm là gốc tọa độ có đường kính bằng

Những câu hỏi liên quan
1.C/m có vô số đường tròn đi qua A và B phân biệt
2.C/m không tồn tại đường tròn đi qua 3 điểm A,B,C thẳng hàng
3.C/m trong vô số đường tròn qua A và B đường tròn nào nhận bán kính nhỏ nhất
Cho đường tròn tâm O và điểm M nằm ngoài đường tròn đó. Qua M kẻ các tiếp tuyến MA, MB với đường tròn (A, B là tiếp điểm). Đường thẳng (d) thay đổi đi qua M, không đi qua O và luôn cắt đường tròn tại hai điểm phân biệt C và D (C nằm giữa M và D).a) Chứng minh AMBO là tứ giác nội tiếp.b) Chứng minh MC.MDMAc) Biết AB 8cm, MO 25 phần 3 . Tính bán kính đường tròn tâm OGiúp tui câu c với nhaaa
Đọc tiếp
Cho đường tròn tâm O và điểm M nằm ngoài đường tròn đó. Qua M kẻ các tiếp tuyến MA, MB với đường tròn (A, B là tiếp điểm). Đường thẳng (d) thay đổi đi qua M, không đi qua O và luôn cắt đường tròn tại hai điểm phân biệt C và D (C nằm giữa M và D).
a) Chứng minh AMBO là tứ giác nội tiếp.
b) Chứng minh MC.MD=MA
c) Biết AB = 8cm, MO = 25 phần 3 . Tính bán kính đường tròn tâm O
Giúp tui câu c với nhaaa
Cho đường tròn tâm O và điểm M nằm ngoài đường tròn đó. Qua M kẻ các tiếp tuyến MA, MB với đường tròn (A, B là tiếp điểm). Đường thẳng (d) thay đổi đi qua M, không đi qua O và luôn cắt đường tròn tại hai điểm phân biệt C và D (C nằm giữa M và D).
a) Chứng minh AMBO là tứ giác nội tiếp.
b) Chứng minh MC.MD=MA\(^2\)
Cho đường tròn tâm O và điểm M nằm ngoài đường tròn đó. Qua M kẻ các tiếp tuyến MA, MB với đường tròn (A, B là tiếp điểm). Đường thẳng (d) thay đổi đi qua M, không đi qua O và luôn cắt đường tròn tại hai điểm phân biệt C và D (C nằm giữa M và D).a) Chứng minh AMBO là tứ giác nội tiếp.b) Chứng minh MC.MDMA2c) Chứng minh đường tròn ngọai tiếp tam giác OPQ luôn đi qua điểm cố định khác O
Đọc tiếp
Cho đường tròn tâm O và điểm M nằm ngoài đường tròn đó. Qua M kẻ các tiếp tuyến MA, MB với đường tròn (A, B là tiếp điểm). Đường thẳng (d) thay đổi đi qua M, không đi qua O và luôn cắt đường tròn tại hai điểm phân biệt C và D (C nằm giữa M và D).
a) Chứng minh AMBO là tứ giác nội tiếp.
b) Chứng minh MC.MD=MA2
c) Chứng minh đường tròn ngọai tiếp tam giác OPQ luôn đi qua điểm cố định khác O
a: góc OAM+góc OBM=180 độ
=>OAMB nội tiếp
b: Xét ΔMAC và ΔMDA có
góc MAC=góc MDA
góc AMC chung
=>ΔMAC đồng dạng với ΔMDA
=>MA/MD=MC/MA
=>MA^2=MD*MC
Đúng 0
Bình luận (0)
1) Viết pt đường tròn tâm l (1,-1) và đi qua điểm B (1,3) 2) Viết pt đường tròn tâm l (3,-4) và đi qua điểm A (1,3) 3) Viết pt đường tròn tâm l ( -2,4) , đi qua điểm B (-6,1) 4) viết pt đường tròn tâm l (1,-2) và đi qua điểm N ( 3,4) Giúp vs bạn
Cho tam giác ABC có 3 góc nhọn, AB < AC và 3 đường cao AD,BE,CF cùng đi qua điểm H. Gọi (S) là đường tròn ngoại tiếp tam giác DEF
1, CM đường tròn (S) đi qua trung điểm của đoạn thẳng AH
2, Gọi M,N lần lượt là giao điểm của đường tròn (S) với các đoạn BH, CH. Tiếp tuyến tại D của đường tròn (S) cắt đường thẳng MN tại T. CM đường thẳng HT song song với EF
1) Gọi G là trung điểm AH
Ta có: \(\angle AFH+\angle AEH=90+90=180\Rightarrow AEHF\) nội tiếp
Tương tự \(\Rightarrow CDHE,AFDC\) nội tiếp
Vì \(\Delta AFH\) vuông tại F có G là trung điểm AH \(\Rightarrow GA=GH=GF\)
Tương tự \(\Rightarrow GE=GA=GH\Rightarrow GE=GF=GA=GH\)
\(\Rightarrow G\) là tâm (AEHF)
Ta có: \(\angle FEH=\angle FAH=\angle FCD=\angle HED\)
\(\Rightarrow\angle FED=2\angle FEH=2\angle FAH=\angle FGD\Rightarrow FGED\) nội tiếp
\(\Rightarrow\left(S\right)\) đi qua trung điểm AH
2) EFMN nội tiếp \(\Rightarrow\angle FNM=\angle FEM=\angle FCB\) (BCEF nội tiếp)
\(\Rightarrow MN\parallel BC\) mà \(BC\bot AD\Rightarrow MN\bot AD\)
MDEG nội tiếp \(\Rightarrow\angle MDG=\angle MEG=\angle HEG=\angle GHE=\angle MHD\)
\(\Rightarrow\Delta MHD\) cân tại M có \(MN\bot HD\Rightarrow MN\) là trung trực HD
mà \(T\in MN\Rightarrow\angle MHT=\angle MDT=\angle MED=\angle FEM\)
\(\Rightarrow HT\parallel EF\)

Đúng 2
Bình luận (0)
Cho đường tròn (O), từ điểm m ngoài đường tròn kẻ 2 tiếp tuyến MA và MB. Đường tròn đi qua M tiếp xúc Với AB tại B cắt đường tròn (O) tại C. Chứng mình CA đi qua trung điểm MB
Cho đường tròn tâm O ,một điểm M nằm ngoài đường tròn.Từ M kẻ đường thẳng đi qua tâm O,cắt đường tròn tại hai điểm A,B (A nằm giữa M và B).Kẻ đường thẳng thứ hai đi qua M,cắt đường tròn tại hai điểm phân biệt C,D (C nằm giữa M và D. C khác A).ĐƯờng thẳng vuông góc với MA tại M cắt đường thẳng BC tại N,đường thẳng NA cắt đường tròn tại điểm thứ 2 là E.a.Chứng minh tứ giác AMNC nội tiếpb.Chứng minh DE vuông góc với MB
Đọc tiếp
Cho đường tròn tâm O ,một điểm M nằm ngoài đường tròn.Từ M kẻ đường thẳng đi qua tâm O,cắt đường tròn tại hai điểm A,B (A nằm giữa M và B).Kẻ đường thẳng thứ hai đi qua M,cắt đường tròn tại hai điểm phân biệt C,D (C nằm giữa M và D. C khác A).ĐƯờng thẳng vuông góc với MA tại M cắt đường thẳng BC tại N,đường thẳng NA cắt đường tròn tại điểm thứ 2 là E.
a.Chứng minh tứ giác AMNC nội tiếp
b.Chứng minh DE vuông góc với MB
a: góc ACB=1/2*sđ cung AB=90 độ
=>ΔACN vuông cân tại C
góc ACN+góc AMN=180 độ
=>AMNC nội tiếp
b: AMNC nội tiếp
=>góc CNA=góc CMA=góc BMD
góc BNE=1/2(sđ cung BE-sđ cung AC)
góc DMB=1/2*(sđ cung BD-sđ cung AC)
=>sđ cung BD=sđ cung BE
=>B nằm trên trung trực của DE
Xét ΔADB và ΔAEB có
góc ADB=góc aEB
AB chung
DB=BE
=>ΔABD=ΔAEB
=>AD=AE
=>A nằm trên trung trực của DE
=>AB là trung trực của DE
=>DE vuông góc AB
Đúng 0
Bình luận (0)
Cho đường tròn (O;R) và một điểm S nằm bên ngoài đường tròn. Kẻ các tiếp tuyến SA,SB của đường tròn (O;R) (với A,B là tiếp điểm). Đường thẳng a đi qua S (không đi qua tâm O) cắt đường tròn(O;R) tại hai điểm M,N (M nằm giữ S và N). a) CM: SO ⊥ AB b) Gọi I là trung điểm của MN và H là giao điểm của SO,AB ;hai đường...
Đọc tiếp
Cho đường tròn (O;R) và một điểm S nằm bên ngoài đường tròn. Kẻ các tiếp tuyến SA,SB của đường tròn (O;R) (với A,B là tiếp điểm). Đường thẳng a đi qua S (không đi qua tâm O) cắt đường tròn(O;R) tại hai điểm M,N (M nằm giữ S và N). a) CM: SO ⊥ AB b) Gọi I là trung điểm của MN và H là giao điểm của SO,AB ;hai đường thẳng OI và AB cắt nahu tại E.CM: OI.OE=R2 (vẽ hộ em hình luôn ạ)
a, Ta có SA = SB (tc tiếp tuyến cắt nhau )
OA = OB = R
Vậy OS là đường trung trực đoạn AB
=> SO vuông AB tại H
b, Vì I là trung điểm
=> OI vuông NS
Xét tứ giác IHSE ta có ^EHS = ^EIS = 900
mà 2 góc này kề, cùng nhìn cạnh ES
Vậy tứ giác IHSE nt 1 đường tròn
=> ^ESH = ^HIO ( góc ngoài đỉnh I )
Xét tam giác OIH và tam giác OSE có
^HIO = ^OSE (cmt)
^O_ chung
Vậy tam giác OIH ~ tam giác OSE (g.g)
\(\dfrac{OI}{OS}=\dfrac{OH}{OE}\Rightarrow OI.OE=OH.OS\)
Xét tam giác OAS vuông tại A ( do SA là tiếp tuyến với A là tiếp điểm), đường cao AH ta có
\(OA^2=OH.OS\)(hệ thức lượng)
\(\Rightarrow OA^2=R^2=OI.OE\)
Đúng 3
Bình luận (0)
Cho đường tròn (O) và điểm A nằm bên ngoài đường tròn (O). Qua điểm A dựng hai tiếp tuyến AM,AN đến đường tròn (O) với M,N là các tiếp điểm. Một đường thẳng d đi qua A cắt đường tròn (O) tại hai điểm B và C (ABAC, đường thẳng d không đi qua tâm O)a) Chứng minh tứ giác AMON là tứ giác nội tiếpb) Chứng minh AN^2AB.ACc) Hai tiếp tuyến của đường trong (O) tại B và C cắt nhau tại K. Chứng minh rằng điểm K luôn thuộc một đường thẳng cố định khi đường thẳng d thay đổi và đường thẳng d thỏa mãn điều kiệ...
Đọc tiếp
Cho đường tròn (O) và điểm A nằm bên ngoài đường tròn (O). Qua điểm A dựng hai tiếp tuyến AM,AN đến đường tròn (O) với M,N là các tiếp điểm. Một đường thẳng d đi qua A cắt đường tròn (O) tại hai điểm B và C (AB<AC, đường thẳng d không đi qua tâm O)
a) Chứng minh tứ giác AMON là tứ giác nội tiếp
b) Chứng minh AN\(^2\)=AB.AC
c) Hai tiếp tuyến của đường trong (O) tại B và C cắt nhau tại K. Chứng minh rằng điểm K luôn thuộc một đường thẳng cố định khi đường thẳng d thay đổi và đường thẳng d thỏa mãn điều kiện đề bài
a: góc AMO+góc ANO=180 độ
=>AMON nội tiếp
b: Xét ΔANB và ΔACN có
góc ANB=góc ACN
góc NAB chung
=>ΔANB đồng dạng với ΔACN
=>AN^2=AB*AC
Đúng 0
Bình luận (0)