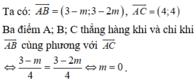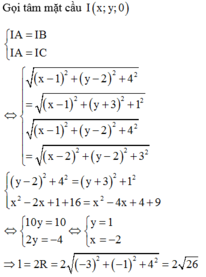Những câu hỏi liên quan
Trong mặt phẳng tọa độ Oxy, cho ba điểm A(3;-1); B(2; 10); C(-4; 2). Tính tích vô hướng
A
B
→
.
A
C
→
.
A.
A
B
→
.
A
C
→
40.
B.
A
B...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho ba điểm A(3;-1); B(2; 10); C(-4; 2). Tính tích vô hướng A B → . A C → .
A. A B → . A C → = 40.
B. A B → . A C → = − 40.
C. A B → . A C → = 26.
D. A B → . A C → = - 26.
Ta có A B → = − 1 ; 11 , A C → = − 7 ; 3 .
Suy ra A B → . A C → = − 1 . − 7 + 11.3 = 40.
Chọn A.
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho ba điểm A(3; -1); B(2; 10); C(-4; 2). Tính tích vô hướng A B → . A C → .
A. 40
B. – 40
C. 26
D. – 26
Ta có A B → = − 1 ; 11 , A C → = − 7 ; 3 .
Suy ra A B → . A C → = − 1 . − 7 + 11.3 = 40.
Chọn A.
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, cho ba điểm A, B, C với B là trung điểm của đoạn thẳng AC. Tìm tọa độ điểm C, biết A(1; 3) và B(2; -1).
\(\left\{{}\begin{matrix}x_B=\dfrac{x_A+x_C}{2}\\y_B=\dfrac{y_A+y_C}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}1+x_C=4\\3+y_C=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_C=3\\y_C=-5\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho ba điểm A(-4; 0); B(-5; 0) và C(3; 0). Tìm điểm M thuộc trục hoành sao cho
M
A
→
+
M
B
→
+
M
C
→
0
→
.
A. M (-2; 0) B. M(2; 0) C. M(- 4; 0) D. M(- 5; 0)
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho ba điểm A(-4; 0); B(-5; 0) và C(3; 0). Tìm điểm M thuộc trục hoành sao cho M A → + M B → + M C → = 0 → .
A. M (-2; 0)
B. M(2; 0)
C. M(- 4; 0)
D. M(- 5; 0)
Ta có M ∈ O x nên M(x;O) và M A → = − 4 − x ; 0 M B → = − 5 − x ; 0 M C → = 3 − x ; 0 ⇒ M A → + M B → + M C → = − 6 − 3 x ; 0 .
Do M A → + M B → + M C → = 0 → nên − 6 − 3 x = 0 ⇔ x = − 2 ⇒ M − 2 ; 0 .
Chọn A.
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, cho ba điểm A (-1;7) ,B (4;-3) và C (-4;1). Hãy viết phương trình đường tròn nội tiếp tam giác ABC
Trong mặt phẳng Oxy, cho A(m-1; -1) ; B(2; 2-2m) ; C(m+3; 3). Tìm giá trị m để A; B; C là ba điểm thẳng hàng?
A. m= 2
B. m=0
C. m=1
D. m=-2
Trong mặt phẳng Oxy, cho ba điểm \(D\left( { - 1;4} \right),E\left( {0; - 3} \right),F\left( {5;0} \right)\)
a) Vẽ các điểm D, E, F trên mặt phẳng Oxy
b) Tìm tọa độ của các vectơ \(\overrightarrow {OD} ,\overrightarrow {OE} ,\overrightarrow {OF} \).
c) Vẽ và tìm tọa độ hai vectơ đơn vị và \(\overrightarrow j \)lần lượt trên hai trục tọa độ Ox và Oy
a)
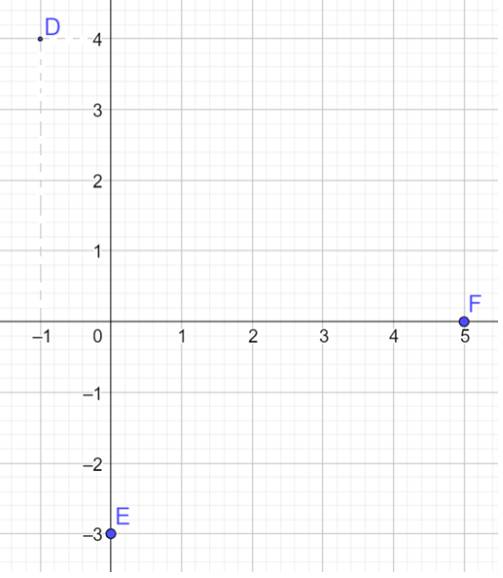
b) Vì tọa độ vectơ \(\overrightarrow {OM} \) chính là tọa độ của điểm M (với mọi M) nên ta có:
\(\overrightarrow {OD} = \left( { - 1;4} \right),\overrightarrow {OE} = \left( {0; - 3} \right),\overrightarrow {OF} = \left( {5;0} \right)\)
c)
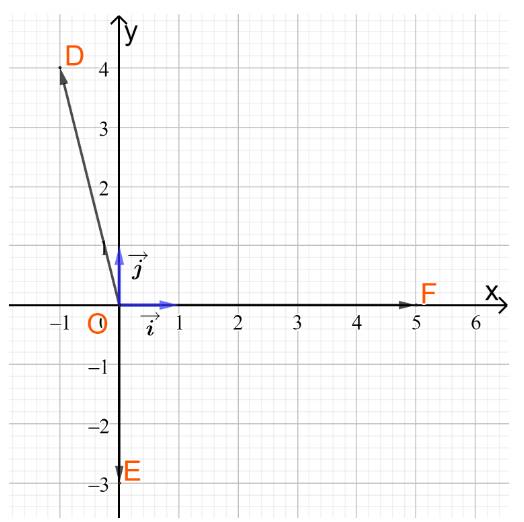
Từ hình vẽ ta có tọa độ của hai vectơ và \(\overrightarrow j \)là
và \(\overrightarrow j = (0;1)\)
Đúng 0
Bình luận (0)
Trong mặt phẳng toạ độ của oxy cho ba điểm A(-2:2) B(2:1) C(1:-3)
Tính AC CB
Tính chu vi tam giác ABC
Xem chi tiết
\(\overrightarrow{AB}=\left(4;-1\right)\Rightarrow AB=\sqrt{4^2+\left(-1\right)^2}=\sqrt{17}\)
\(\overrightarrow{AC}=\left(3;-5\right)\Rightarrow AC=\sqrt{3^2+\left(-5\right)^2}=\sqrt{34}\)
\(\overrightarrow{CB}=\left(1;4\right)\Rightarrow BC=\sqrt{1^2+4^2}=\sqrt{17}\)
Chu vi: \(AB+AC+BC=2\sqrt{17}+\sqrt{34}\)
Đúng 0
Bình luận (0)
6) Trong mặt phẳng tọa độ Oxy cho đường thẳng (d): y = - 2/3 x và các điểm A(3;-1),B(-6;4),C( 3/4 ; -1/2 ) Chứng minh rằng ba điểm A, B, C thẳng hàng
\(\overrightarrow{AB}=\left(-9;5\right)\)
\(\overrightarrow{AC}=\left(-\dfrac{9}{4};\dfrac{1}{2}\right)\)
Vì \(\overrightarrow{AB}=k\cdot\overrightarrow{AC}\) nên A,B,C thẳng hàng
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(1;2;-4), B(1;-3;1), C(2;2;3). Tính đường kính l của mặt cầu (S) đi qua 3 điểm trên và có tâm nằm trêm mặt phẳng (Oxy).
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(1;2;-4), B(1;-3;1), C(2;2;3). Tính đường kính l của mặt cầu (S) đi qua 3 điểm trên và có tâm nằm trêm mặt phẳng (Oxy).
![]()
![]()
![]()
![]()