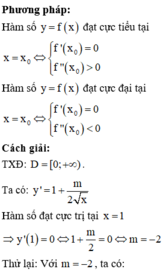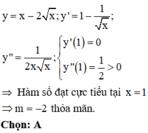Xác định tham số m sao cho hàm số y = x +m\(\sqrt{x}\) đạt cực trị tại x = 1

Những câu hỏi liên quan
Xác định giá trị của tham số m sao cho hàm số y = x + m x đạt cực trị tại x = 1
A. m = -2
B. m = 2
C. m = 6
D. m = -6
Cho hàm số y = f(x) xác định trên tập số thực R và có đạo hàm f'(x) = (x - sinx)(x- m- 3)(x- \(\sqrt{9-m^2}\) )3 ∀x∈ R (m là tham số). Có bao nhiêu giá trị nguyên của m để hàm số y =f(x) đạt cực tiểu tại x = 0
\(f'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x-sinx=0\\x-m-3=0\\x-\sqrt{9-m^2}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=m+3\\x=\sqrt{9-m^2}\end{matrix}\right.\)
Do hệ số bậc cao nhất của x dương nên:
- Nếu \(m=-3\Rightarrow f'\left(x\right)=0\) có nghiệm bội 3 \(x=0\) \(\Rightarrow x=0\) là cực tiểu (thỏa mãn)
- Nếu \(m=3\Rightarrow x=0\) là nghiệm bội chẵn (không phải cực trị, ktm)
- Nếu \(m=0\Rightarrow x=3\) là nghiệm bội chẵn và \(x=0\) là nghiệm bội lẻ, đồng thời \(x=0\) là cực tiểu (thỏa mãn)
- Nếu \(m\ne0;\pm3\) , từ ĐKXĐ của m \(\Rightarrow-3< m< 3\Rightarrow\left\{{}\begin{matrix}m+3>0\\\sqrt{9-m^2}>0\end{matrix}\right.\)
Khi đó \(f'\left(x\right)=0\) có 3 nghiệm pb trong đó \(x=0\) là nghiệm nhỏ nhất
Từ BBT ta thấy \(x=0\) là cực tiểu
Vậy \(-3\le m< 3\)
Đúng 2
Bình luận (3)
Xác định giá trị của tham số m để hàm số m để hàm số y = x 3 + m x + 1 x + m đạt giá trị cực đại tại x = 2.
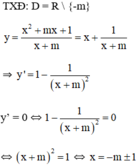
Ta có bảng biến thiên:
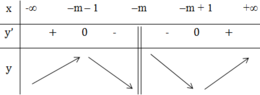
Dựa vào BBT thấy hàm số đạt cực đại tại x = -m – 1.
Hàm số đạt cực đại tại x = 2 ⇔ -m – 1 = 2 ⇔ m = -3.
Vậy m = -3.
Đúng 0
Bình luận (0)
Bài 1. Cho hàm số: y 1/3 x3 - mx2 +(m2 - m + 1)x + 1. Với giá trị nào của m thì hàm số đạt cực đại tại điểm x 1Bài 2. Cho hàm số y 1/3 x3 + (m2 - m + 2) x2 + (3m2 + 1)x + m - 5. Tìm m để hàm số đạt cực tiểu tại x -2 .Bài 3. Cho hàm số y 1/3 x3 - (m+1) x2 + (m2 + 2m)x + 1 (m là tham số). Tìm tất cả tham số thực m để hàm số đạt cực tiểu tại x 2.Bài 4. Tìm tất cả tham số thực m để hàm số y (m-1)x4 - (m2 - 2) x2 + 2016 đạt cực tiểu tạix -1.Bài 5. Tìm giá trị của tham số m để hàm số y x3/3...
Đọc tiếp
Bài 1. Cho hàm số: y = 1/3 x3 - mx2 +(m2 - m + 1)x + 1. Với giá trị nào của m thì hàm số đạt cực đại tại điểm x = 1
Bài 2. Cho hàm số y = 1/3 x3 + (m2 - m + 2) x2 + (3m2 + 1)x + m - 5. Tìm m để hàm số đạt cực tiểu tại x = -2 .
Bài 3. Cho hàm số y = 1/3 x3 - (m+1) x2 + (m2 + 2m)x + 1 (m là tham số). Tìm tất cả tham số thực m để hàm số đạt cực tiểu tại x = 2.
Bài 4. Tìm tất cả tham số thực m để hàm số y = (m-1)x4 - (m2 - 2) x2 + 2016 đạt cực tiểu tại
x = -1.
Bài 5. Tìm giá trị của tham số m để hàm số y = x3/3 +(2m - 1)x2 + (m - 9)x + 1 đạt cực tiểu tại
x = 2 .
Đừng hỏi tại sao tui ngu!!!
Giúp.com.vn
Xác định m để hàm số: y = x 3 − m x 2 + (m – 2/3)x + 5 có cực trị tại x = 1. Khi đó, hàm số đạt cực tiểu hay đạt cực đại? Tính cực trị tương ứng.
Ta biết hàm số y = f(x) có cực trị khi phương trình y’ = 0 có nghiệm và y’ đổi dấu khi qua các nghiệm đó.
Ta có:
Xét y’ = 0, ta có: y′ = 3 x 2 − 2mx + (m – 2/3)
∆ ’ > 0 khi m < 1 hoặc m > 2 (∗)
Để hàm số có cực trị tại x = 1 thì
y′(1) = 3 − 2m + m – 2/3 = 0 ⇔ m = 7/3, thỏa mãn điều kiện (∗)
Với m = 7/3 thì hàm số đã cho trở thành:
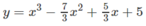
Ta có:
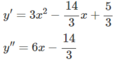
Vì y′′(1) = 6 – (14/3) > 0 nên hàm số đạt cực tiểu tại x = 1 và y CT = y(1) = (16/3).
Đúng 0
Bình luận (0)
Xác định m để hàm số: y = x 3 − m x 2 + (m – 2/3)x + 5 có cực trị tại x = 1. Khi đó, hàm số đạt cực tiểu hay đạt cực đại? Tính cực trị tương ứng.
Ta biết hàm số y = f(x) có cực trị khi phương trình y’ = 0 có nghiệm và y’ đổi dấu khi qua các nghiệm đó.
Ta có:
Xét y’ = 0, ta có: y′ = 3 x 2 − 2mx + (m – 2/3)
Δ’ > 0 khi m < 1 hoặc m > 2 (∗)
Để hàm số có cực trị tại x = 1 thì
y′(1) = 3 − 2m + m – 2/3 = 0 ⇔ m = 7/3, thỏa mãn điều kiện (∗)
Với m = 7/3 thì hàm số đã cho trở thành:
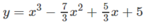
Ta có:
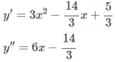
Vì y′′(1) = 6 – (14/3) > 0 nên hàm số đạt cực tiểu tại x = 1 và y C T = y(1) = (16/3).
Đúng 0
Bình luận (0)
Xác định giá trị của tham số m để hàm số y = x 3 – 2 x 2 + mx + 1 đạt cực tiểu tại x = 1. (Đề thi tốt nghiệp THPT năm 2011)
TXĐ: D = R
y’ = 3 x 2 – 4x + m; y’ = 0 ⇔ 3 x 2 – 4x + m = 0
Phương trình trên có hai nghiệm phân biệt khi:
∆ ’ = 4 – 3m > 0 ⇔ m < 4/3 (∗)
Hàm số có cực trị tại x = 1 thì :
y’(1) = 3 – 4 + m = 0 ⇒ m = 1 (thỏa mãn điều kiện (∗) )
Mặt khác, vì:
y’’ = 6x – 4 ⇒ y’’(1) = 6 – 4 = 2 > 0
cho nên tại x = 1, hàm số đạt cực tiểu.
Vậy với m = 1, hàm số đã cho đạt cực tiểu tại x = 1
Đúng 0
Bình luận (0)
Xác định giá trị của tham số m để hàm số y = x 3 – 2 x 2 + mx + 1 đạt cực tiểu tại x = 1. (Đề thi tốt nghiệp THPT năm 2011)
TXĐ: D = R
y’ = 3 x 2 – 4x + m; y’ = 0 ⇔ 3 x 2 – 4x + m = 0
Phương trình trên có hai nghiệm phân biệt khi:
∆’ = 4 – 3m > 0 ⇔ m < 4/3 (∗)
Hàm số có cực trị tại x = 1 thì :
y’(1) = 3 – 4 + m = 0 ⇒ m = 1 (thỏa mãn điều kiện (∗) )
Mặt khác, vì:
y’’ = 6x – 4 ⇒ y’’(1) = 6 – 4 = 2 > 0
cho nên tại x = 1, hàm số đạt cực tiểu.
Vậy với m = 1, hàm số đã cho đạt cực tiểu tại x = 1
Đúng 0
Bình luận (0)
Cho hàm số
y
m
3
x
3
+
(
m
-
2
)
x
2
+
(
m
-
1
)
x
+
2
, với
m
là tham số thực. Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số đạt cực đại tại điểm
x
1
và đạt...
Đọc tiếp
Cho hàm số y = m 3 x 3 + ( m - 2 ) x 2 + ( m - 1 ) x + 2 , với m là tham số thực. Tìm tất cả các giá trị thực của tham số m sao cho hàm số đạt cực đại tại điểm x 1 và đạt cực tiểu tại điểm x 2 thỏa mãn x 1 < x 2
A. 0 < m < 4 3
B. m ≤ 0
C. 5 4 < m < 4 3
D. Không tồn tại m thỏa mãn