Cho a là số bất kì, \(P=\dfrac{2a}{a^2+1}\). BĐT nào sau đây đúng vs mọi a
A. P>-1 B.P>1 C.P<-1 D.\(P\le1\)
Những câu hỏi liên quan
Câu 1:Cho tập hợp P các số tự nhiên nhỏ hơn 6.Câu nào sai?
A.P={0,1,2,3,4,5} B.P={X THUỘC X/X <6}
C.P={X THUỘC N/X<-5} D.P={X THUỘC N/X<5}
Câu 2:Số nào sau đây là ước chung của 24và30?
A.6 B.5 C.4 D.8
Cho a, b là 2 số dương bất kì. Mệnh đề nào sau đây đúng? A.
log
a
b
b
log
a
B.
log
a
b
log
a
.
log
b
C.
log
a
+
b
log
a
+
log
...
Đọc tiếp
Cho a, b là 2 số dương bất kì. Mệnh đề nào sau đây đúng?
A. log a b = b log a
B. log a b = log a . log b
C. log a + b = log a + log b
D. log a b = log a log b
CMR với mọi số nguyên a,b,c ta đều có BĐT:
\(\dfrac{a^2}{\left(2a+b\right)\left(2a+c\right)}+\dfrac{b^2}{\left(2b+a\right)\left(2b+c\right)}+\dfrac{c^2}{\left(2c+a\right)\left(2c+b\right)}\le\dfrac{1}{3}\)
Gọi a là số thực lớn nhất để bất phương trình
x
2
-
x
+
2
+
a
ln
(
x
2
-
x
+
1
)
≥
0
nghiệm đúng với mọi x. Mệnh đề nào sau đây đúng? A. . B. . C. . D. .
Đọc tiếp
Gọi a là số thực lớn nhất để bất phương trình x 2 - x + 2 + a ln ( x 2 - x + 1 ) ≥ 0 nghiệm đúng với mọi x. Mệnh đề nào sau đây đúng?
A. 
.
B. 
.
C. 
.
D. 
.
Đáp án B
Đặt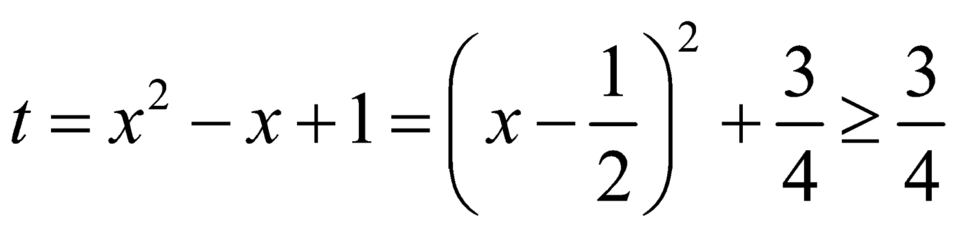 
Ta có:
Đặt 
.
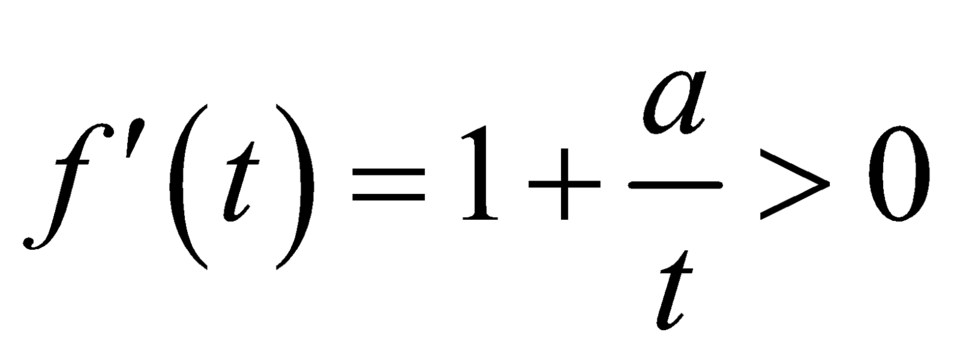
là hàm số đồng biến trên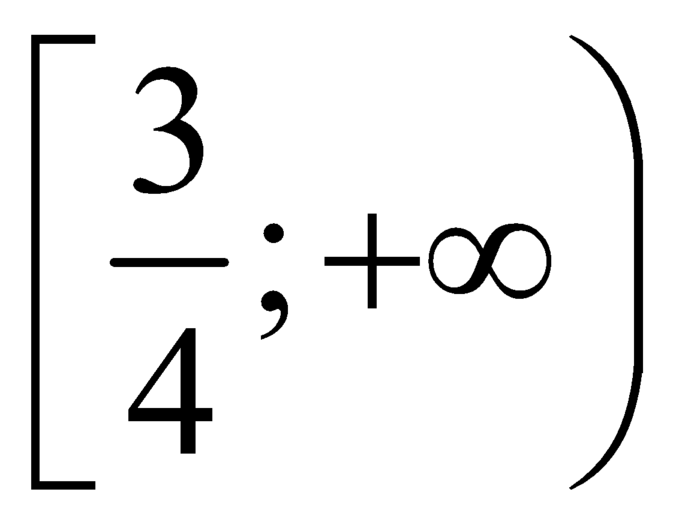 
.
Khi đó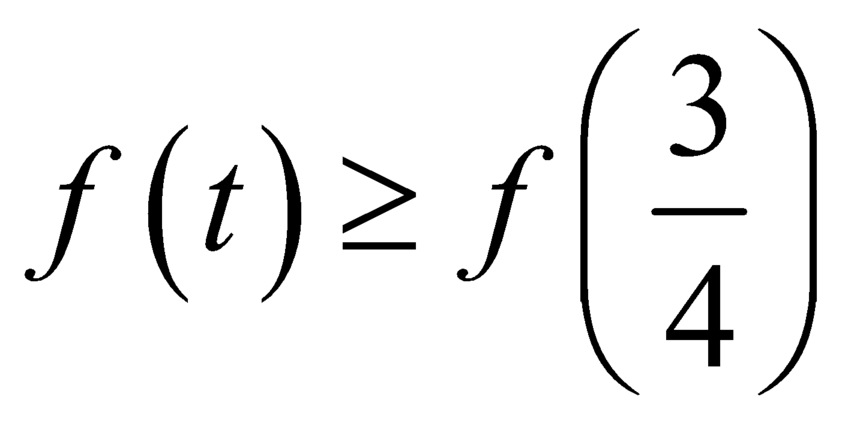 
Đúng 0
Bình luận (0)
Cho bất phương trình \(\left|x^2+x+a\right|+\left|x^2-x+a\right|\le2x\left(1\right)\) Khi đó khẳng định nào sau đây đúng nhất?
A. (1) có nghiệm khi \(a\le\dfrac{1}{4}\)
B. Mọi nghiện của (1) đều không âm.
C. (1) có nghiệm lớn hơn 1 khi a<0
D. Tất cả đều đúng
(làm theo hình thức tự luận)
Cho a, b, c, d là các số thực dương, khác 1 bất kì. Mệnh đề nào dưới đây đúng A.
a
c
b
d
⇔
ln
a
ln
b
c...
Đọc tiếp
Cho a, b, c, d là các số thực dương, khác 1 bất kì. Mệnh đề nào dưới đây đúng
A. a c = b d ⇔ ln a ln b = c d
B. a c = b d ⇔ ln a ln b = d c
C. a c = b d ⇔ ln a b = d c
D. a c = b d ⇔ ln a b = c d
1. Rút gọn biểu thức Pcos^4x-sin^4xA.Pcos2x B.Pdfrac{3}{4}+dfrac{1}{4}cos4x C.Pdfrac{1}{4}+dfrac{3}{4}cos4x D.Pdfrac{3}{4}-dfrac{1}{4}cos4x2.Đơn giản biểu thức Dsinleft(dfrac{5pi}{2}-alpharight)+cosleft(13pi+alpharight)-3sinleft(alpha-5piright)A.3sina-2cosa B.3sina C.-3sina D.2cosa+3sinaTrắc nghiệm nhưng mong mn trình bày bài làm giúp em để tham khảo với ạ. Em cảm ơn
Đọc tiếp
1. Rút gọn biểu thức \(P=cos^4x-sin^4x\)
\(A.P=cos2x\) \(B.P=\dfrac{3}{4}+\dfrac{1}{4}cos4x\) \(C.P=\dfrac{1}{4}+\dfrac{3}{4}cos4x\) \(D.P=\dfrac{3}{4}-\dfrac{1}{4}cos4x\)
2.Đơn giản biểu thức \(D=sin\left(\dfrac{5\pi}{2}-\alpha\right)+cos\left(13\pi+\alpha\right)-3sin\left(\alpha-5\pi\right)\)
\(A.3sina-2cosa\) \(B.3sina\) \(C.-3sina\) \(D.2cosa+3sina\)
Trắc nghiệm nhưng mong mn trình bày bài làm giúp em để tham khảo với ạ. Em cảm ơn
1.Ý A
\(P=cos^4x-sin^4x=\left(cos^2x-sin^2x\right)\left(cos^2x+sin^2x\right)=cos2x\)
2. Ý B
\(D=sin\left(\dfrac{5\pi}{2}-\alpha\right)+cos\left(13\pi+\alpha\right)-3sin\left(\alpha-5\pi\right)\)
\(=sin\left(2\pi+\dfrac{\pi}{2}-\alpha\right)+cos\left(\pi+\alpha+12\pi\right)-3sin\left(\alpha+\pi-6\pi\right)\)
\(=sin\left(\dfrac{\pi}{2}-\alpha\right)+cos\left(\pi+\alpha\right)-3sin\left(\alpha+\pi\right)\)
\(=cos\alpha-cos\alpha+3sin\alpha=3sin\alpha\)
Đúng 1
Bình luận (0)
Gọi a là số thực lớn nhất để bất phương trình
x
2
-
x
+
2
+
a
ln
x
2
-
x
+
1
≥
0
nghiệm đúng với mọi
x
∈
ℝ
. Mệnh đề nào sau đây đúng? A.
a
∈
(
2
;
3...
Đọc tiếp
Gọi a là số thực lớn nhất để bất phương trình x 2 - x + 2 + a ln x 2 - x + 1 ≥ 0 nghiệm đúng với mọi x ∈ ℝ . Mệnh đề nào sau đây đúng?
A. a ∈ ( 2 ; 3 ]
B. a ∈ 8 ; + ∞
C. a ∈ ( 6 ; 7 ]
D. a ∈ ( - 6 ; - 5 ]
Chọn đáp án C
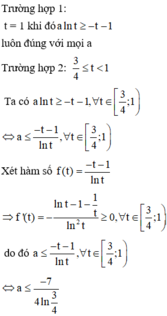
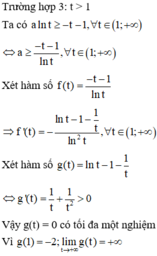
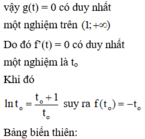
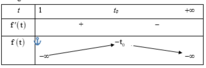
Vậy số thực a thỏa mãn yêu cầu bài toán là: a ∈ ( 6 ; 7 ]
Đúng 0
Bình luận (0)
Gọi a là số thực lớn nhất để bất phương trình
x
2
−
x
−
2
+
a
ln
x
2
−
x
+
1
≥
0
nghiệm đúng với mọi
x
∈
ℝ
.
Mệnh đề nào sau đây đúng? A.
a
∈
6...
Đọc tiếp
Gọi a là số thực lớn nhất để bất phương trình x 2 − x − 2 + a ln x 2 − x + 1 ≥ 0 nghiệm đúng với mọi x ∈ ℝ . Mệnh đề nào sau đây đúng?
A. a ∈ 6 ; 7 .
B. a ∈ 2 ; 3 .
C. a ∈ − 6 ; − 5 .
D. a ∈ 8 ; + ∞
Đáp án A.
Đặt t = x 2 − x + 1 = x − 1 2 2 + 3 4 ≥ 3 4
Khi đó BPT trở thành
f t = t + 1 + a ln t ≥ 0
Ta có: f ' t = + ∞ ; f 3 4 = 3 4 + a ln 3 4
Với a > 0 ⇒ f t đồng biến trên
3 4 ; + ∞ ⇒ f t ≥ 0 ∀ t ∈ 3 4 ; + ∞ ⇔ M i n 3 4 ; + ∞ f t = 7 4 + a
⇔ a ln 3 4 ≥ − 7 4 ⇔ a ≤ − 7 4 ln 3 4 ≈ 6 , 08.
Vì đề bài yêu cầu tìm số thực lớn nhất
nên suy ra a ∈ 6 ; 7 .
Đúng 0
Bình luận (0)