Một bộ bài có 52 lá, hãy tính xác xuất để 2 lần xáo bài trùng nhau.

Những câu hỏi liên quan
Một bộ bài tú lơ khơ gồm 52 lá bài. Rút ngẫu nhiên 5 lá, tính xác xuất để rút được 5 lá: 10, J, Q, K, A đồng chất
Xem chi tiết
Lời giải:
Rút 5 trong 52 lá bài, có $C^5_{52}$ kết quả.
Rút 5 lá 10, J, Q, K, A đồng chất, có 4 kết quả (bích, tép, cơ, rô)
Xác suất rút được 5 lá thỏa mãn đề: $\frac{4}{C^5_{52}}$
Đúng 0
Bình luận (0)
Rút ra một lá bài từ bộ bài 52 lá. Xác suất để được lá bích là:
A. 1/13
B. 1/4
C. 12/13
D. 3/4
Số phần tử không gian mẫu: n(Ω) = 52
Số phần tử của biến cố xuất hiện lá bích n(A) = 13
Suy ra 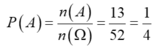
Chọn B.
Đúng 0
Bình luận (0)
Rút ra một lá bài từ bộ bài 52 lá. Xác suất để được lá át (A) là:
A. 2/13
B.1/169
C. 1/13
D. 3/4.
Số phần tử không gian mẫu: n(Ω)=52
Số phần tử của biến cố xuất hiện lá át n(A)=4
Suy ra 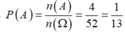
Chọn C.
Đúng 0
Bình luận (0)
Rút ra một lá bài từ bộ bài 52 lá. Xác suất để được lá J màu đỏ hay lá là:
A.1/13
B. 3/26
C. 3/13
D. 1/128
Số phần tử không gian mẫu: n(Ω)=52
Số phần tử của biến cố xuất hiện lá J đỏ hay lá 5 là n(A)=2+4=6
Suy ra 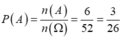
Chọn B.
Đúng 0
Bình luận (0)
Rút ra một lá bài từ bộ bài 52 lá. Xác suất để được lá át (A) hay lá rô là:
A. 1/52
B. 2/13
C. 4/13
D. 17/52
Số phần tử không gian mẫu: n(Ω) = 52
Số phần tử của biến cố xuất hiện lá át hay lá rô n(A) = 4 +12 = 16.
Suy ra 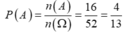
Chọn C.
Đúng 0
Bình luận (0)
Xét một bộ bài 52 lá. Nếu những lá bài này được đánh dấu bằng các số nguyên khác nhau, hỏi xác suất để các lá bài này được sắp xếp theo một dãy số nguyên tăng dần là bao nhiêu ?
rút ngẫu nhiên 2 con bài từ bộ bài 52 lá. TÍnh xác suất để lấy được quân K.
Không gian mẫu: \(C_{52}^2\)
Số cách rút không có quân K nào: \(C_{48}^2\)
Xác suất: \(P=\dfrac{C_{52}^2-C_{48}^2}{C_{52}^2}=...\)
Đúng 2
Bình luận (0)
Rút ngẫu nhiên đồng thời 2 lá bài từ bộ bài 52 lá. Tính xác suất rút được 2 lá bài cơ biết rằng hai lá này màu đỏ
Gọi A là biến cố "Rút được 2 lá bài cơ".
Số kết quả thuận lợi là \(\left|\Omega_A\right|=C^2_{13}=78\).
Số kết quả có thể xảy ra là \(\left|\Omega\right|=C^2_{52}=1326\).
\(\Rightarrow\) Xác suất xảy ra biến cố A là \(P\left(A\right)=\dfrac{78}{1326}=\dfrac{1}{17}\).
Đúng 0
Bình luận (0)
Rút ngẫu nhiên 1 lá bài từ bộ bài tây 52 lá. Tính xác suất của biến cố “Lá bài được chọn có màu đỏ hoặc là lá có số chia hết cho 5”.
Gọi \(A\) là biến cố “Hạt giống thứ nhất nảy mầm”, \(B\) là biến cố “Hạt giống thứ hai nảy mầm”.
\(P\left( A \right) = P\left( B \right) = 0,8 \Rightarrow P\left( {\bar A} \right) = P\left( {\bar B} \right) = 1 - 0,8 = 0,2\)
Xác suất để có đúng 1 trong 2 hạt giống đó nảy mầm là:
\(P\left( {A\bar B} \right) + P\left( {\bar AB} \right) = P\left( A \right).P\left( {\bar B} \right) + P\left( {\bar A} \right).P\left( B \right) = 0,8.0,2 + 0,2.0,8 = 0,32\)
Đúng 0
Bình luận (0)















