Những câu hỏi liên quan
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn O các đường cao AM , BN cho tam giác ABC cắt nhau tại H và cắt đường tròn lần lượt tại D và E Chứng minh A, tứ giác MHNC nội tiếp đường tròn B, CD = CE C, CB là tia phân giác của góc HCD
a: góc HMC+góc HNC=180 độ
=>HMCN nội tiếp
b: góc CED=góc CAD
góc CDE=góc CAE
mà góc CAD=góc CAE(=góc CBD)
nên góc CED=góc CDE
=>CD=CE
Đúng 0
Bình luận (0)
Cho tam giác ABC nội tiếp đường tròn O. Tia phân giác của góc A cắt BC ở D và cắt đường tròn tại M. Đường phân giác của góc ngoài đỉnh A của tam giác ABC cắt đường tròn ở N. CMR:
a) Góc BMC= góc ABC + góc ACB
b) OM vuông góc với BC
c) M; O; N thẳng hàng
d) AD.AM = AB.AC
e) MB.MC=MD.MA.
Cho tam giác ABC nội tiếp đường tròn tâm O. Tia phân giác của góc A cắt
đường tròn tại E, tia phân giác của góc B cắt đường tròn tại F; AE cắt BF tại
K; EF cắt CB, CA lần lượt lại Q và P, CK cắt PQ tại G. Chứng minh:
a) EF là tia phân giác của góc AEC.
b) Tam giác AKF cân F.
c) Tam giác ECK cân tại E.
d) G là trung điểm của PQ
Cho tam giác ABC nội tiếp đường tròn tâm O. Các tia phân giác của các góc A và B cắt nhau ở I và cắt đường tròn theo thứ tự ở D và E. Chứng minh:a, Tam giác BDI là tam giác cânb, DE là đường trung trực của ICc, IF và BC song song, trong đó F là giao điểm của DE và AC
Đọc tiếp
Cho tam giác ABC nội tiếp đường tròn tâm O. Các tia phân giác của các góc A và B cắt nhau ở I và cắt đường tròn theo thứ tự ở D và E. Chứng minh:
a, Tam giác BDI là tam giác cân
b, DE là đường trung trực của IC
c, IF và BC song song, trong đó F là giao điểm của DE và AC
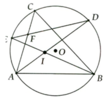
a, B I D ^ = 1 2 s đ D E ⏜ = D B E ^ => ∆BID cân ở D
b, Chứng minh tương tự: DIEC cân tại E, DDIC cân tại D
=> EI = EC và DI = DC
=> DE là trung trực của CI
c, F Î DE nên FI = FC
=> F I C ^ = F C I ^ = I C B ^ => IF//BC
Đúng 1
Bình luận (0)
cho tam giác ABC nội tiếp đường tròn tâm O. Các tia phân giác góc A và B cắt hau ở I và cắt đường tròn theo thứ tự ở D và E. Chứng minh
a) tam BDI là tam giác cân
b)DE là trung trực của IC
c) IF và BC song song, trong đó F là giao điểm DE và AC
Xem chi tiết
Cho tam giác cân ABC (AB = AC) nội tiếp đường tròn (O). Các đường phân giác của hai góc B và C cắt nhau ở E và cắt đường tròn lần lượt ở F và D. Chứng minh rằng tứ giác EDAF là một hình thoi ?
giúp mk vs ạ:cho tam giác ABC cân nội tiếp đường tròn O. các đường phân giác góc B và góc C cắt nhau ở E và cắt đường tròn lần lượt ở F và D. Chứng minh rằng tứ giác EDAF là hình thoi
Cho tam giác cân ABC (AB = AC) nội tiếp đường tròn (O). Các đường phân giác của hai góc B và C cắt nhau ở E và cắt đường tròn lần lượt tại F và D. Chứng minh rằng tứ giác EDAF là một hình thoi
Cho tam giác ABC nội tiếp đường tròn (O), tia phân giác của góc A cắt đường tròn ở M. Tiếp tuyến kẻ từ M với đường tròn cắt các tia AB và AC lần lượt tại D và E. Chứng minh: a/ BC song song với DE b/ Tam giác AMB đồng dạng tam giác MCE c/ Tam giác AMC đồng dạng tam giác MDB d/ Nếu AC=CE thì MA^2 = MD.ME