a, B I D ^ = 1 2 s đ D E ⏜ = D B E ^ => ∆BID cân ở D
b, Chứng minh tương tự: DIEC cân tại E, DDIC cân tại D
=> EI = EC và DI = DC
=> DE là trung trực của CI
c, F Î DE nên FI = FC
=> F I C ^ = F C I ^ = I C B ^ => IF//BC
Đúng 1
Bình luận (0)
Các câu hỏi tương tự
cho tam giác ABC nội tiếp đường tròn tâm O. Các tia phân giác góc A và B cắt hau ở I và cắt đường tròn theo thứ tự ở D và E. Chứng minha) tam BDI là tam giác cânb)DE là trung trực của ICc) IF và BC song song, trong đó F là giao điểm DE và AC
Xem chi tiết
cho tam giác ABC nội tiếp đường tròn tâm O. Các tia phân giác góc A và B cắt hau ở I và cắt đường tròn theo thứ tự ở D và E. Chứng minh
a) tam BDI là tam giác cân
b)DE là trung trực của IC
c) IF và BC song song, trong đó F là giao điểm DE và AC
Xem chi tiết
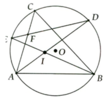
Cho tam giác ABC nội tiếp đường tròn tâm O . Các tia phân giác của các góc A và B cắt nhau ở I và cắt đường tròn theo thứ tự ở D và E . Chứng minh rằng :
a) tam giác: BDI là tam giác cân .
b) DE là đường trung trực của IC .
C)IF//BC ( F là giao điểm của DE và AC ).
Cho tam giác ABC nội tiếp đường tròn tâm O. Các tia phân giác của các góc A và B cắt nhau ở I và cắt đường tròn theo thứ tự ở D và E. Gọi F là giao điểm của AC với DE. Chứng minh rằng:
a) Tam giác BDI là tam giác cân
b) DE là đường trung trực của IC
c) IF song song BC
Cho tam giác ABC nội tiếp đường tròn tâm O.Các tia phân giác của góc A và B cắt nhau tại I và cắt đường tròn theo thứ tụ tại D và E
a.BDI cân
b.DE là đường trung trực của IC
c. IF //BC ( F là giao điểm của DE và AC )
Cho tam giác ABC và nội tiếp đường tròn O . Phân giác góc A và góc B cắt nhau tại I cắt đường tròn lần lượt tại D và E , gọi F là giao điểm của AC và DE . CMR
a, tam giác BID cân
b, DE là trung trực của IC
c, IFsong song BC
( giúp mình nhanh vs ạ mình đang cần gấp :(((
Cho tam giác ABC nội tiếp đường tròn tâm O.Các tia phân giác của góc A và B cắt nhau tại I và cắt đường tròn theo thứ tụ tại D và E
a.ΔΔBDI cân
DE là đường trung trực của IC
c. IF //BC ( F là giao điểm của DE và AC )
cho tam giác nhọn ABC nội tiếp đường tròn (O). Hai đường phân giác trong của góc A và góc B cắt nhau ở I và thứ tự cắt đường tròn ở D và E. Đường thẳng DE cắt BC và AC lần lượt ở M và N. Chứng minh:
a) tứ giác AENI và BIMD nội tiếp
b) tứ giác CMIN là hình thoi
Cho tam giác ABC nội tiếp đường tròn (O), tia phân giác của góc A cắt đường tròn ở M. Tiếp tuyến kẻ từ M với đường tròn cắt các tia AB và AC lần lượt tại D và E. Chứng minh: a/ BC song song với DE b/ Tam giác AMB đồng dạng tam giác MCE c/ Tam giác AMC đồng dạng tam giác MDB d/ Nếu AC=CE thì MA^2 = MD.ME