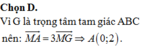Trong mặt phẳng với hệ tọa độ Oxy, cho A(3;1), B(-1;2). Cho điểm M di động trên đường thẳng d: y=x. Đường thẳng MA cắt trục hoành tại P và đường thẳng MB cắt trục tung tại Q. Chứng minh đường thẳng PQ luôn đi qua một điểm cố định

Những câu hỏi liên quan
Trong mặt phẳng tọa độ với hệ tọa độ Oxy, cho hai điểm A(-2,3), B(1,-6). Tọa độ vecto AB là?
\(\overrightarrow{AB}=\left(x_B-x_A;y_B-y_A\right)=\left(3;-9\right)\)
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) có phương trình là
x
-
z
-
3
0
. Tính góc giữa (P) và mặt phẳng (Oxy) A. 30
°
B. 60
°
C. 45
°
D. 90
°
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) có phương trình là x - z - 3 = 0 . Tính góc giữa (P) và mặt phẳng (Oxy)
A. 30 °
B. 60 °
C. 45 °
D. 90 °
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(-2;4), B(4;1), C(-2;-1). Tìm tọa độ trực tâm H tam giác.
vecto AH=(x+2;y-4); vecto BC=(-6;-2)
vecto BH=(x-4;y-1); vecto AC=(0;-5)
Theo đề, ta có: -6(x+2)-2(y-4)=0 và 0(x-4)-5(y-1)=0
=>y=1 và -6(x+2)=2(y-4)=2*(1-4)=-6
=>x+2=1 và y=1
=>x=-1 và y=1
Đúng 1
Bình luận (0)
trong mặt phẳng với hệ tọa độ Oxy, cho hình thang cân ABCD ( AB//CD) . biết tọa độ các điểm A(-8;2) B(-4;6)D(-6-8) xác định tọa độ đỉnh C
\(\overrightarrow{AB}=\left(-4;4\right)=-4\left(1;-1\right)\)
\(\Rightarrow\) Phương trình CD song song AB đi qua D có dạng:
\(1\left(x+6\right)+1\left(y+8\right)=0\Leftrightarrow x+y+14=0\)
Gọi M là trung điểm AB \(\Rightarrow M\left(-6;4\right)\)
Phương trình đường thẳng d qua M và vuông góc AB có dạng:
\(1\left(x+6\right)-1\left(y-4\right)=0\Leftrightarrow x-y+10=0\)
Gọi N là giao điểm CD và d \(\Rightarrow\) N là trung điểm CD do ABCD là hình thang cân
Tọa độ N là nghiệm: \(\left\{{}\begin{matrix}x+y+14=0\\x-y+10=0\end{matrix}\right.\) \(\Rightarrow N\left(-12;-2\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_C=2x_N-x_D=...\\y_C=2y_N-y_D=...\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, mặt phẳng qua điểm A(1;2;3) và song song với mặt phẳng toạ độ (Oxy) có phương trình là
A. x-1=0.
B. y-2=0.
C. z+3=0.
D. z-3=0.
Trong không gian với hệ tọa độ Oxy cho mặt phẳng
α
:
2
x
-
y
-
3
z
4
. Gọi A ,B ,C lần lượt là giao điểm của mặt phẳng
α
với các trục tọa độ Ox, Oy, Oz. Thể tích tứ diện OABC bằng: A. 1. B. 2. C.
32
9
D.
16
9
Đọc tiếp
Trong không gian với hệ tọa độ Oxy cho mặt phẳng α : 2 x - y - 3 z = 4 . Gọi A ,B ,C lần lượt là giao điểm của mặt phẳng α với các trục tọa độ Ox, Oy, Oz. Thể tích tứ diện OABC bằng:
A. 1.
B. 2.
C. 32 9
D. 16 9
Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có trọng tâm G 2 3 ; 0 , biết M(1;1) là trung điểm cạnh BC. Tọa độ đỉnh A là:
A.(2;0)
B.(-2;0)
C.(0;-2)
D.(0;2)
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(2;-3;7), B(0;4;-3), C(4;2;5). Tìm tọa độ điểm M trên mặt phẳng (Oxy) sao cho
M
A
→
+
M
B
→
+
M
C
→
có g...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(2;-3;7), B(0;4;-3), C(4;2;5). Tìm tọa độ điểm M trên mặt phẳng (Oxy) sao cho M A → + M B → + M C → có giá trị nhỏ nhất
A. M(-2;-1;0)
B. M(-2;-1;0)
C. M(2;-1;0)
D. M(2;1;0)
Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có trọng tâm
G
(
2
3
;
0
)
, biết
M
(
1
;
1
)
là trung điểm cạnh BC. Tọa độ đỉnh A là: A. (2;0) B. (-2;0) C. (0;-2) D. (0;2)
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có trọng tâm G ( 2 3 ; 0 ) , biết M ( 1 ; 1 ) là trung điểm cạnh BC. Tọa độ đỉnh A là:
A. (2;0)
B. (-2;0)
C. (0;-2)
D. (0;2)
Trong không gian với hệ tọa độ Oxy cho mặt phẳng (P): z-2x+3=0. Một vecto pháp tuyến của (P) là:
A. (0;1;-2)
B. (1;-2;3)
C. (2;0;-1)
D. (1;-2;0)