Tìm nghiệm nguyên của phương trình:x6+3x2+1=y4

Những câu hỏi liên quan
Tìm nghiệm nguyên của phương trình sau
x3+x2y+2xy3=x2y2+y4
Tìm nghiệm nguyên của phương trình: 3x2 + 13xy + 26(x − y) + 39y2 = 2022
Bài 1 : tìm x ; y nguyên dương
2xy + x + y = 83
Bài 2 tìm nghiệm nguyên của phương trình :
a ) x2 + 2y2 + 3xy - x - y + 3 = 0
b ) 6x2y3 + 3x2 - 10y3 = -2
Cho đa thức: Q(x) = x4 + 3x2 + 1
a. Phân tích đa thức Q(x) thành nhân tử.
b. Tìm nghiệm nguyên của phương trình y2 = x4 + 3x2 + 1.
\(3x^2+4x+1=3x^2+3x+x+1=\left(x+1\right)\left(3x+1\right)\)
Đúng 0
Bình luận (0)
Cho phương trình 3x2-c=a(x2-2x+1)-b(x-1) tìm 3 số nguyên a,b,c để phương trình có nghiệm với mọi x thược R.
=>3x^2-c=ax^2-2ax+a-bx+b
=>3x^2-c-a*x^2+2ax-a+bx-b=0
=>x^2(3-a)+x(2a+b)-a-b-c=0
Để phương trình luôn có nghiệm thì 3-a=0 và 2a+b=0 và a+b+c=0
=>a=3; b=-6; c=-a-b=-3+6=3
Đúng 0
Bình luận (1)
Tìm tập nghiệm của phương trình
3
x
2
+
2
x
1
. A.
S
-
1
;
3
B.
S
0
;
-
2
C.
S...
Đọc tiếp
Tìm tập nghiệm của phương trình 3 x 2 + 2 x = 1 .
A. S = - 1 ; 3
B. S = 0 ; - 2
C. S = 1 ; - 3
D. S = 0 ; 2
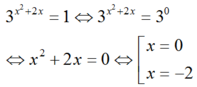
Vậy tập nghiệm của phương trình là S = 0 ; - 2
Chọn B.
Đúng 0
Bình luận (0)
Tìm tập nghiệm của phương trình 3 x 2 + 2 x = 1 .
A.S={-1;3}
B. S = {0;2}
C. S = {1;-3}
D. S = {0;2}
Cho phương trình: 3x2 + 5x – 1 = 0 (1). Gọi x1 , x2 là hai nghiệm (nều
có) của phương trình (1). Không tìm x1 , x2 hãy tính K = (3x1 – 1)(3x2 – 1) + 3
Ta có: \(\Delta=5^2-5.3.1=25-12=13>0\)
Suy ra pt luôn có 2 nghiệm phân biệt
Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=-5\\x_1x_2=-1\end{matrix}\right.\)
\(K=\left(3x_1-1\right)\left(3x_2-1\right)+3\\ =3x_1x_2-3x_2-3x_1+1+3=3.\left(-1\right)-3\left(x_1+x_2\right)+4\\ =-3+4-3\left(-5\right)\\ =1+15\\ =16\)
Đúng 0
Bình luận (1)
\(\Delta=25-4\left(-1\right).3=25+12=37>0\)
vậy pt luôn có 2 nghiệm pb
Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{5}{3}\\x_1x_2=-\dfrac{1}{3}\end{matrix}\right.\)
Ta có \(K=9x_1x_2-3\left(x_1+x_2\right)+4\)
Thay vào ta được \(K=9\left(-\dfrac{1}{3}\right)-3\left(-\dfrac{5}{3}\right)+4=-3+5+4=6\)
Đúng 0
Bình luận (1)
Tìm tập nghiệm của phương trình
3
x
2
+
4
x
−
1
27
A.
−
2
B.
−
2
−
2
2...
Đọc tiếp
Tìm tập nghiệm của phương trình 3 x 2 + 4 x − 1 = 27
A. − 2
B. − 2 − 2 2 ; − 2 + 2 2
C. − 2 − 7 ; − 2 + 7
D. − 2 + 2 2
Đáp án B
PT ⇔ x 2 + 4 x − 1 = 3 ⇔ x 2 + 4 x − 4 = 0 ⇔ x = − 2 + 2 2 x = − 2 − 2 2 ⇒ S = − 2 − 2 2 ; − 2 + 2 2
Đúng 0
Bình luận (0)
Cho phương trình
2
-
m
3
-
3
m
2
+
1
.
log
81
x...
Đọc tiếp
Cho phương trình 2 - m 3 - 3 m 2 + 1 . log 81 x 3 - 3 x 2 + 1 + 2 + 2 - x 3 - 3 x 2 + 1 - 2 . log 3 1 m 3 - 3 m 2 + 1 + 2 = 0 . Gọi S là tập hợp tất cả các giá trị m nguyên để phương trình đã cho có số nghiệm thuộc đoạn 6 ; 8 . Tính tổng bình phương tất cả các phần tử của tập S.
A. 20
B. 28
C. 14
D. 10