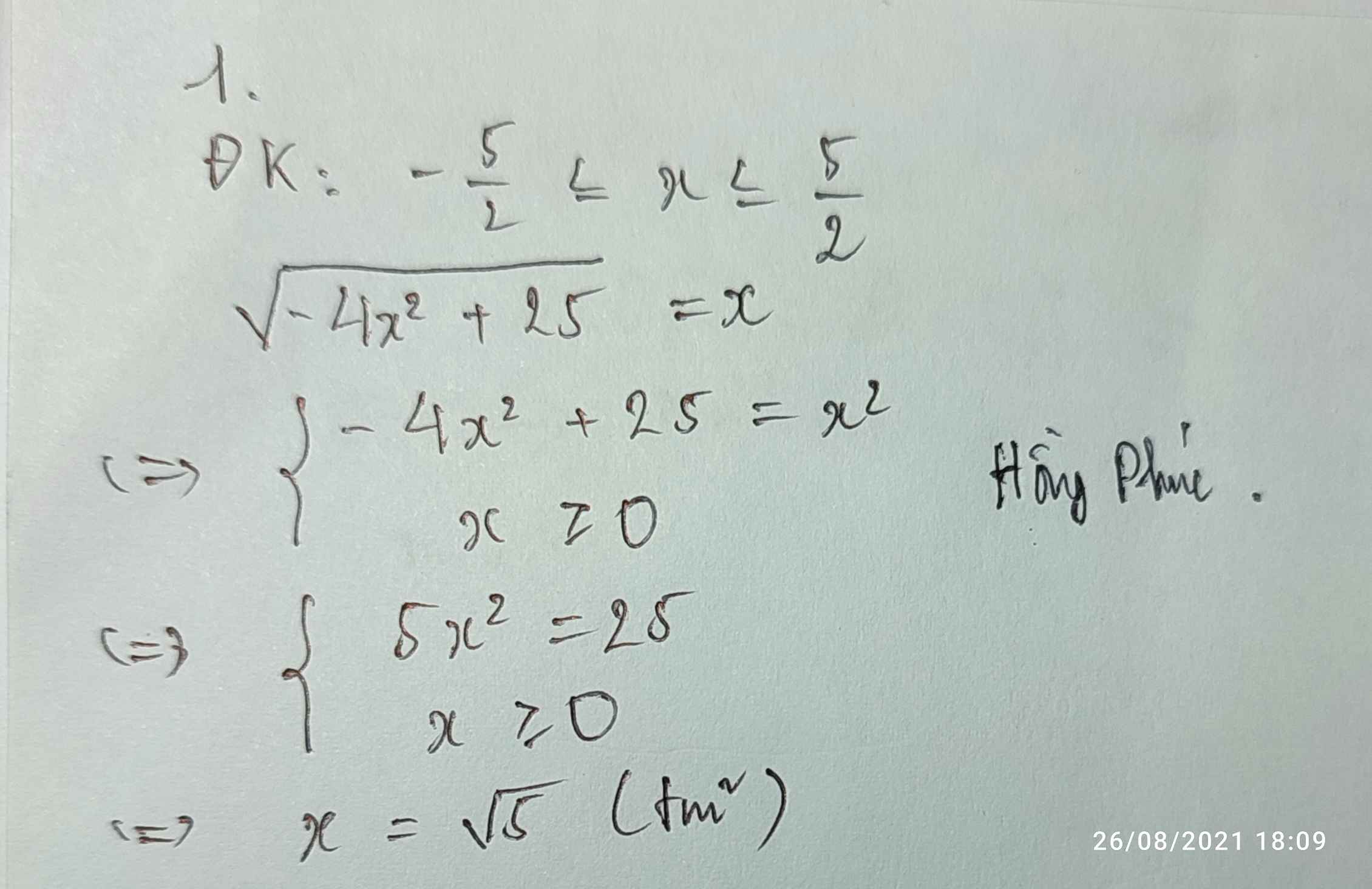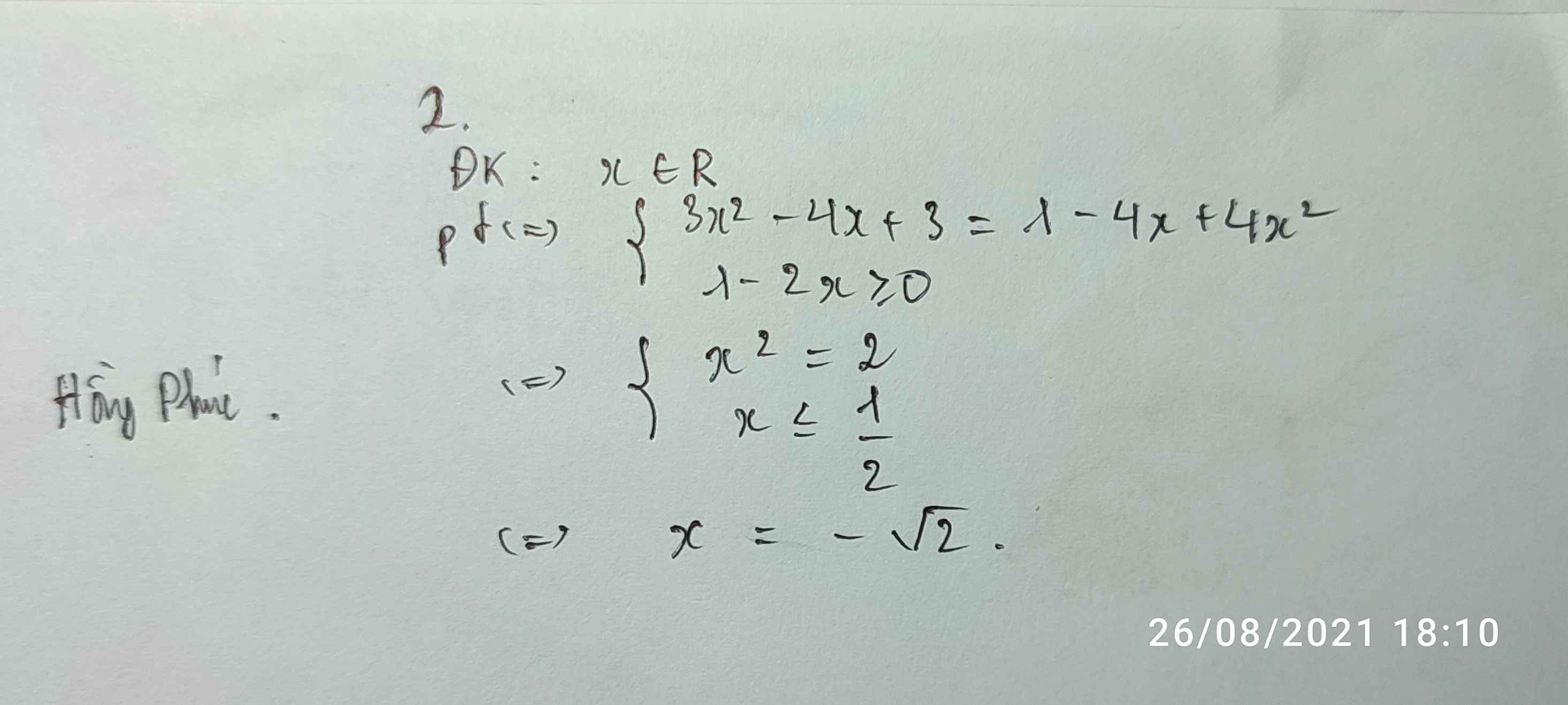f) Ta có: \(\sqrt{16\left(x+1\right)}-\sqrt{9\left(x+1\right)}=4\)

\(\Leftrightarrow4\left|x+1\right|-3\left|x+1\right|=4\)

\(\Leftrightarrow\left|x+1\right|=4\)

\(\Leftrightarrow\left[{}\begin{matrix}x+1=4\\x+1=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-5\end{matrix}\right.\)

g) Ta có: \(\sqrt{9x+9}+\sqrt{4x+4}=\sqrt{x+1}\)

\(\Leftrightarrow5\sqrt{x+1}-\sqrt{x+1}=0\)

\(\Leftrightarrow x+1=0\)

hay x=-1

a.

Kiểm tra lại đề bài, đề bài không đúng

b.

ĐKXĐ: \(x\ge0\)

\(1+3\sqrt{x}=4x+\sqrt{x+2}\)

\(\Rightarrow4x-1-\left(3\sqrt{x}-\sqrt{x+2}\right)=0\)

\(\Leftrightarrow4x-1-\dfrac{2\left(4x-1\right)}{3\sqrt{x}+\sqrt{x+2}}=0\)

\(\Leftrightarrow\left(4x-1\right)\left(1-\dfrac{2}{3\sqrt{x}+\sqrt{x+2}}\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}4x-1=0\Rightarrow x...\\3\sqrt{x}+\sqrt{x+2}=2\left(1\right)\end{matrix}\right.\)

Xét (1): \(\Leftrightarrow10x+2+6\sqrt{x^2+2x}=4\)

\(\Leftrightarrow3\sqrt{x^2+2x}=1-5x\) (\(x\le\dfrac{1}{5}\))

\(\Leftrightarrow16x^2-28x+1=0\Rightarrow x=\dfrac{7-3\sqrt{5}}{8}\)

1: ĐKXĐ: x>1/2

=>\(\dfrac{x}{\sqrt{2x-1}}+\dfrac{x}{\sqrt[4]{4x-3}}=2\)

x^2-2x+1>=0

=>x^2>=2x-1

=>\(\dfrac{x}{\sqrt{2x-1}}>=1\)

Dấu = xảy ra khi x=1

(x^2-2x+1)(x^2+2x+3)>=0

=>x^4-4x+3>=0

=>x^4>=4x-3

=>\(\dfrac{x}{\sqrt[4]{4x-3}}>=1\)

=>VT>=2

Dấu = xảy ra khi x=1

2: 4x-1=x+x+2x-1

5x-2=x+2x-1+2x-1

\(\left(\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{2x-1}}\right)\left(\sqrt{x}+\sqrt{x}+\sqrt{2x-1}\right)>=9\)

=>\(\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{2x-1}}>=\dfrac{9}{\sqrt{x}+\sqrt{x}+\sqrt{2x-1}}\)

\(\left(\sqrt{x}+\sqrt{x}+\sqrt{2x-1}\right)^2< =3\left(4x-1\right)\)

=>\(\sqrt{x}+\sqrt{x}+\sqrt{2x-1}< =\sqrt{3\left(4x-1\right)}\)

=>\(\dfrac{2}{\sqrt{x}}+\dfrac{1}{\sqrt{2x-1}}>=\dfrac{3\sqrt{3}}{\sqrt{4x-1}}\)

Tương tự, ta cũng có: \(\dfrac{1}{\sqrt{x}}+\dfrac{2}{\sqrt{2x-1}}>=\dfrac{3\sqrt{3}}{\sqrt{5x-2}}\)

=>\(\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{2x-1}}>=\sqrt{3}\left(\dfrac{1}{\sqrt{4x-1}}+\dfrac{1}{\sqrt{5x-2}}\right)\)

Dấu = xảy ra khi x=1

\(a) \sqrt{4x^2− 9} = 2\sqrt{x + 3}\)

\(ĐK:x\ge\dfrac{3}{2}\)

\(pt\Leftrightarrow4x^2-9=4\left(x+3\right)\)

\(\Leftrightarrow4x^2-9=4x+12\)

\(\Leftrightarrow4x^2-4x-21=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1-\sqrt{22}}{2}\left(l\right)\\x=\dfrac{1+\sqrt{22}}{2}\left(tm\right)\end{matrix}\right.\)

\(b)\sqrt{4x-20}+3.\sqrt{\dfrac{x-5}{9}}-\dfrac{1}{3}\sqrt{9x-45}=4\)

\(ĐK:x\ge5\)

\(pt\Leftrightarrow2\sqrt{x-5}+\sqrt{x-5}-\sqrt{x-5}=4\)

\(\Leftrightarrow2\sqrt{x-5}=4\Leftrightarrow\sqrt{x-5}=2\)

\(\Leftrightarrow x-5=4\Leftrightarrow x=9\left(tm\right)\)

\(c)\dfrac{2}{3}\sqrt{9x-9}-\dfrac{1}{4}\sqrt{16x-16}+27.\sqrt{\dfrac{x-1}{81}}=4\)

ĐK:x>=1

\(pt\Leftrightarrow2\sqrt{x-1}-\sqrt{x-1}+3\sqrt{x-1}=4\)

\(\Leftrightarrow4\sqrt{x-1}=4\Leftrightarrow\sqrt{x-1}=1\)

\(\Leftrightarrow x-1=1\Leftrightarrow x=2\left(tm\right)\)

\(d)5\sqrt{\dfrac{9x-27}{25}}-7\sqrt{\dfrac{4x-12}{9}}-7\sqrt{x^2-9}+18\sqrt{\dfrac{9x^2-81}{81}}=0\)

\(ĐK:x\ge3\)

\(pt\Leftrightarrow3\sqrt{x-3}-\dfrac{14}{3}\sqrt{x-3}-7\sqrt{x^2-9}+6\sqrt{x^2-9}=0\)

\(\Leftrightarrow-\dfrac{5}{3}\sqrt{x-3}-\sqrt{x^2-9}=0\Leftrightarrow\dfrac{5}{3}\sqrt{x-3}+\sqrt{x^2-9}=0\)

\(\Leftrightarrow(\dfrac{5}{3}+\sqrt{x+3})\sqrt{x-3}=0\)

\(\Leftrightarrow\sqrt{x-3}=0\)    (vì \(\dfrac{5}{3}+\sqrt{x+3}>0\))

\(\Leftrightarrow x-3=0\Leftrightarrow x=3\left(nhận\right)\)

\(a=\lim\limits_{x\rightarrow0}\dfrac{\sqrt{4x+1}-1+1-\sqrt[3]{2x+1}}{x}\)

\(=\lim\limits_{x\rightarrow0}\dfrac{\dfrac{4x}{\sqrt[]{4x+1}+1}+\dfrac{-2x}{1+\sqrt[3]{2x+1}+\sqrt[3]{\left(2x+1\right)^2}}}{x}\)

\(=\lim\limits_{x\rightarrow0}\left(\dfrac{4}{\sqrt[]{4x+1}+1}+\dfrac{-2}{1+\sqrt[3]{2x+1}+\sqrt[3]{\left(2x+1\right)^2}}\right)=...\)

\(b=\lim\limits_{x\rightarrow1}\dfrac{4\left(x-1\right)\left(\sqrt[3]{\left(5x+3\right)^2}+2\sqrt[3]{5x+3}+4\right)}{5\left(x-1\right)\left(\sqrt[]{4x+5}+3\right)}\)

\(=\lim\limits_{x\rightarrow1}\dfrac{4\left(\sqrt[3]{\left(5x+3\right)^2}+2\sqrt[3]{5x+3}+4\right)}{5\left(\sqrt[]{4x+5}+3\right)}=...\)

\(c=\lim\limits_{x\rightarrow-1}\dfrac{\left(2x+3\right)^{\dfrac{1}{4}}+\left(2+3x\right)^{\dfrac{1}{3}}}{\left(x+2\right)^{\dfrac{1}{2}}-1}\)

\(=\lim\limits_{x\rightarrow-1}\dfrac{\dfrac{1}{2}\left(2x+3\right)^{-\dfrac{3}{4}}+\left(2+3x\right)^{-\dfrac{2}{3}}}{\dfrac{1}{2}\left(x+2\right)^{-\dfrac{1}{2}}}=3\)