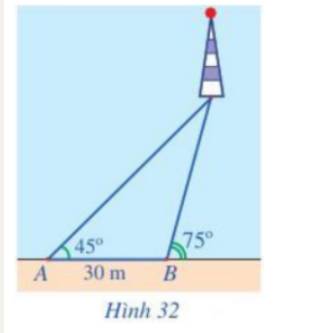
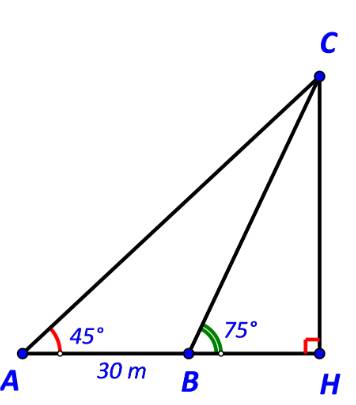
ba ngọn hải đăng phát ra ba kí hiệu khác nhau .hai dấu hiêu liên tiếp của hải đăng A cách nhau 16 giây hải đăng B 45 giây hải đăng C là 150 giây .đúng 18 giờ cả ba đấu hiêu phát ra cùng một lúc . hỏi lúc mấy giờ thì cả ba đấu hiệu cùng phát ra một lúc