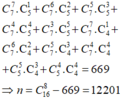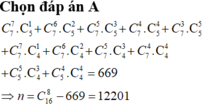Một hộp đựng 8 viên bi xanh,5 viên bi đỏ,4 viên bi vàng;các viên bi chỉ khác nhau về màu.Lấy ngẫu nhiên từ hộp 8 viên bi.Tính xác suất để trong 8 bi đó có 2 viên bi xanh

Những câu hỏi liên quan
Một hộp đựng 7 viên bi xanh, 5 viên bi đỏ và 4 viên bi vàng. Có bao nhiêu cách lấy ra 8 viên bi có đủ 3 màu? A. 12201 B. 10224 C. 12422 D. 14204
Đọc tiếp
Một hộp đựng 7 viên bi xanh, 5 viên bi đỏ và 4 viên bi vàng. Có bao nhiêu cách lấy ra 8 viên bi có đủ 3 màu?
A. 12201
B. 10224
C. 12422
D. 14204
Một hộp đựng 7 viên bi xanh, 5 viên bi đỏ và 4 viên bi vàng. Có bao nhiêu cách lấy ra 8 viên bi có đủ 3 màu?
A. 12201
B. 10224
C. 12422
D. 14204
Một hộp đựng viên bi có tổng 150 viên bi gồm có 4 màu: xanh,đỏ,vàng,trắng.Trong đó,số viên bi xanh bằng 2/15 tổng số viên bi, số viên bi đỏ bằng 1/5 tổng số viên bi: số viên bi vàng bằng số viên bi trắng.Em hãy tính số viên bi mỗi màu có trong hộp đựng viên bi đó?
Số viên bi xanh là :
\(150\times\dfrac{2}{15}=20\) ( viên bi )
Số viên bi đỏ là :
\(150\times\dfrac{1}{5}=30\) ( viên bi )
Tổng số viên bi vàng và tráng là :
\(150-20-30=100\) ( viên bi )
Theo như đề bài, số viên bi vàng bằng số viên bi trắng nên
Có \(100:2=50\) số viên bi vàng
Có \(100:2=50\) số viên bi trắng
Đ/s: ...
Đúng 3
Bình luận (0)
có một hộp đựng 5 viên bi xanh ,6 viên bi đỏ và 4 viên bi vàng a)có bao nhiêu cách lấy ra 6 viên bi ,trong đó có 2 viên bi xanh và có nhiều nhất 2 viên bi vàng và phải có đủ 3 màu. b)có bao nhiêu cách lấy ra 9 viên bi đủ 3 màu
a: Số cách chọn là:
\(C^2_5\cdot C^1_4\cdot C^3_6+C^2_5\cdot C^2_4\cdot C^2_6=1700\left(cách\right)\)
b: Số cách chọn 9 viên bất kì là: \(C^9_{15}\left(cách\right)\)
Số cách chọn 9 viên ko có đủ 3 màu là:
\(C^9_9+C^9_{11}+C^9_{10}=66\left(cách\right)\)
=>Có 4939 cách
Đúng 1
Bình luận (0)
Có một hộp đựng 5 viên bi xanh, 6 viên bi đỏ và 4 viên bi vàng. Có bao nhiêu cách lấy ra 9 viên bi có đủ 3 màu.
A: 2492
B: 1246
C: 4984
D: tất cả sai
Sử dụng phương pháp gián tiếp:
Lấy ra 9 viên bi trong 15 viên bi bất kỳ, có C 15 9 cách.
Trường hợp 1: lấy 9 viên bi chỉ có 2 màu là xanh và đỏ, có C 11 9 cách.
Trường hợp 2: lấy 9 viên bi chỉ có 2 màu là xanh và vàng, có C 9 9 cách.
Trường hợp 3: lấy ra 9 viên bi chỉ có màu đỏ và vàng, có C 10 9 cách.
Vậy có : C 15 9 - ( C 11 9 + C 9 9 + C 10 9 ) = 4984 cách.
Chọn C.
Đúng 0
Bình luận (0)
Có một hộp đựng 5 viên bi xanh, 6 viên bi đỏ và 4 viên bi vàng.Có bao nhiêu cách lấy ra 6 viên bi, trong đó có 2 viên bi xanh và có nhiều nhất 2 viên bi vàng và phải có đủ 3 màu.
A.1500
B.1600
C.372
D. 1700
Các trường hợp xảy ra theo yêu cầu đề:
Trường hơp 1: 2 xanh, 2 vàng, 2 đỏ, có: ![]() cách.
cách.
Trường hợp 2: 2 xanh,1 vàng, 3 đỏ, có: ![]() cách.
cách.
Vậy có : ![]() cách.
cách.
Chọn D.
Đúng 0
Bình luận (0)
Có một số viên bi ( đỏ , xanh , vàng , trắng) đựng trong bốn hộp và đều nhau . Lấy một số viên bi đỏ ở hộp thứ nhất , lấy số viên bi ở hộp thứ hai màu xanh gấp 2 lần số viên đỏ , lấy số viên ở hộp thứ ba bi màu vàng gấp 3 lần số viên bi màu đỏ , lấy số viên bi màu trắng ở hộp thứ tư gấp 4 lần số viên bi màu đỏ . Số viên bi còn lại ở bốn hộp là 50 , số viên bi màu trắng còn lại là 2 . Hỏi bốn hộp có tất cả bao nhiên viên bi ?
Đọc tiếp
Có một số viên bi ( đỏ , xanh , vàng , trắng) đựng trong bốn hộp và đều nhau . Lấy một số viên bi đỏ ở hộp thứ nhất , lấy số viên bi ở hộp thứ hai màu xanh gấp 2 lần số viên đỏ , lấy số viên ở hộp thứ ba bi màu vàng gấp 3 lần số viên bi màu đỏ , lấy số viên bi màu trắng ở hộp thứ tư gấp 4 lần số viên bi màu đỏ . Số viên bi còn lại ở bốn hộp là 50 , số viên bi màu trắng còn lại là 2 . Hỏi bốn hộp có tất cả bao nhiên viên bi ?
Hộp bi thứ nhất có 4 viên bi đỏ, 3 viên bi vàng và 5 viên bi xanh. Hộp bi thứ hai có 2 viên bi đỏ, 6 viên bi vàng và 7 viên bi xanh. Chọn ngẫu nhiên mỗi hộp 2 viên bi, tính xác suất sao cho 4 viên bi được chọn luôn có bi đỏ nhưng không có bi xanh. A.181/231 B.181/2310 C.181/2301 D. tất cả sai
Đọc tiếp
Hộp bi thứ nhất có 4 viên bi đỏ, 3 viên bi vàng và 5 viên bi xanh. Hộp bi thứ hai có 2 viên bi đỏ, 6 viên bi vàng và 7 viên bi xanh. Chọn ngẫu nhiên mỗi hộp 2 viên bi, tính xác suất sao cho 4 viên bi được chọn luôn có bi đỏ nhưng không có bi xanh.
A.181/231
B.181/2310
C.181/2301
D. tất cả sai
Không gian mẫu là chọn ngẫu nhiên mỗi hộp 2 viên bi.
Suy ra số phần tử của không gian mẫu là ![]() .
.
Gọi A là biến cố 4 viên bi được chọn luôn có bi đỏ nhưng không có bi xanh . Ta liệt kê các trường hợp thuận lợi của không gian biến cố A như sau:
● Trường hợp 1. Chọn hộp thứ nhất 2 viên bi đỏ, có ![]() cách.
cách.
Chọn hộp thứ hai 2 viên bi từ 8 viên bi (2 đỏ và 6 vàng), có ![]() cách.
cách.
Do đó trường hợp này có ![]() cách.
cách.
● Trường hợp 2. Chọn hộp thứ nhất 1 viên bi đỏ và 1 viên bi vàng, có ![]() cách.
cách.
Chọn hộp thứ hai 2 viên bi từ 8 viên bi (2 đỏ và 6 vàng), có ![]() cách.
cách.
Do đó trường hợp này có ![]() cách.
cách.
● Trường hợp 3. Chọn hộp thứ nhất 2 viên bi vàng, có ![]() cách.
cách.
Chọn hộp thứ hai 2 viên bi đỏ hoặc 1 viên bi đỏ và 1 viên bi vàng, có ![]() cách.
cách.
Do đó trường hợp này có ![]() cách.
cách.
Suy ra số phần tử của biến cố A là ![]()
Vậy xác suất cần tính 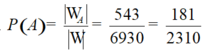
Chọn B.
Đúng 1
Bình luận (0)
một hộp đựng 100 viên bi trong đó có 25 viên bi đỏ,30 viên bi xanh ,35 viên bi vàng,6 viên bi đen,4 viên bi trắng.Hỏi phải lấy ra ít nhất số viên bi để chắc chắn có ít nhất 5 viên bi khác màu?????
ít nhất cần phải lấy ra 97 viên để chắc chắn có ít nhất 5 viên bi khác màu
Đúng 0
Bình luận (0)