Xác định hàm số
(P): y=ax2+bx+5 (a khác 0) biết (P) tiếp xúc trục hoành tại điểm có hoành độ bằng 0
Những câu hỏi liên quan
Tính a2 + b2 + c2 biết hàm số y = ax2 + bx +c (a khác 0) đạt giá trị nhỏ nhất bằng -1/4 khi x = 5/2 và đồ thị cắt trục Ox tại hai điểm sao cho tích hai hoành độ bằng 6
Đồ thị của hàm số
f
x
x
3
+
a
x
2
+
b
x
+
c
tiếp xúc với trục hoành tại gốc tọa độ và cắt đường thẳng x 1 tại điểm có tung độ bằng 3 khi A. a b 0; c 2 B. a c 0; b 2 C. a 2; b c 0 D. a 2; b 1; c 0
Đọc tiếp
Đồ thị của hàm số f x = x 3 + a x 2 + b x + c tiếp xúc với trục hoành tại gốc tọa độ và cắt đường thẳng x = 1 tại điểm có tung độ bằng 3 khi
A. a = b = 0; c = 2
B. a = c = 0; b = 2
C. a = 2; b = c = 0
D. a = 2; b = 1; c = 0
Xác định parabol:
P
:
y
a
x
2
+
b
x
+
c
biết (P) có giá trị lớn nhất bằng 3 tại x2 và cắt trục Ox tại điểm có hoành độ bằng 1 A.
y
-
x
2
+
4
x
-
3
B.
y
x
2
-
4
x...
Đọc tiếp
Xác định parabol: P : y = a x 2 + b x + c biết (P) có giá trị lớn nhất bằng 3 tại x=2 và cắt trục Ox tại điểm có hoành độ bằng 1
A. y = - x 2 + 4 x - 3
B. y = x 2 - 4 x + 7
C. y = 2 x 2 - 12 x + 20
D. y = - 3 x 2 + 12 x - 9
Xác định hàm số y = ax + b (a khác 0) biết:
a) Đồ thị của nó đi qua A(1;2) và song song với đường thẳng y= -x-2
b) Đồ thị của nó cắt trục tung tại điểm có tung độ bằng -2 và cắt trục hoành tại điểm có hoành độ bằng -2
a.
Do ĐTHS song song với \(y=-x-2\Rightarrow a=-1\)
Do đồ thị qua A nên:
\(a.1+b=2\Rightarrow b=2-a=3\)
Vậy pt hàm số có dạng: \(y=-x+3\)
b.
Do đồ thị hàm số cắt trục tung tại điểm có tung độ bằng -2 nên:
\(-2=a.0+b\Rightarrow b=-2\)
Do ĐTHS cắt trục hoành tại điểm có hoành độ -2
\(\Rightarrow0=a.\left(-2\right)+b\Rightarrow a=\dfrac{b}{2}=-1\)
Vậy hàm số có dạng: \(y=-x-2\)
Đúng 1
Bình luận (0)
Xác định y=ax+b. biết đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 5, cắt trục hoành tại điểm có hoành độ bằng -3
Cho hàm số y x3 + ax2 + bx + c đi qua điểm A(0;-4) và đạt cực đại tại điểm B(1;0) hệ số góc k của tiếp tuyến với đồ thị hàm số tại điểm có hoành độ bằng -1 là: A. k 0 B. k 24 C. k -18 D. k 18
Đọc tiếp
Cho hàm số y = x3 + ax2 + bx + c đi qua điểm A(0;-4) và đạt cực đại tại điểm B(1;0) hệ số góc k của tiếp tuyến với đồ thị hàm số tại điểm có hoành độ bằng -1 là:
A. k = 0
B. k = 24
C. k = -18
D. k = 18
Đáp án B
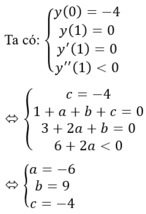
Do đó k = y’(-1) = 3 – 2a + b = 24.
Đúng 0
Bình luận (0)
Xác định hàm số y = ax + b , biết đồ thị cắt trục tung tại điểm có tung độ bằng 5 và cắt trục hoành tại điểm có hoành độ bằng -3
PT giao Ox tại hoành độ -3: \(y=0;x=-3\Leftrightarrow-3a+b=0\left(1\right)\)
PT giao Oy tại tung độ 5: \(y=5;x=0\Leftrightarrow b=5\left(2\right)\)
\(\left(1\right)\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{5}{3}\\b=5\end{matrix}\right.\Leftrightarrow y=\dfrac{5}{3}x+5\)
Đúng 0
Bình luận (0)
Xác định a, b, c biết parabol y = ax2 + bx + c Có đỉnh I(-1 ; -4) và cắt trục tung tại điểm có hoành độ =-3
giúp mình với
Sửa đề: cắt trục tung tại điểm có tung độ bằng -3
Thay x=0 và y=-3 vào (P), ta được:
\(a\cdot0^2+b\cdot0+c=-3\)
=>0+0+c=-3
=>c=-3
vậy: (P): \(y=ax^2+bx-3\)
Tọa độ đỉnh là I(-1;-4) nên ta có:
\(\left\{{}\begin{matrix}-\dfrac{b}{2a}=-1\\-\dfrac{b^2-4\cdot a\cdot\left(-3\right)}{4a}=-4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=2a\\\dfrac{b^2+12a}{4a}=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=2a\\\left(2a\right)^2+12a=16a\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=2a\\4a^2-4a=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=2a\\4a\left(a-1\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=2a\\\left[{}\begin{matrix}a=0\left(loại\right)\\a-1=0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho hàm số
y
x
3
+
a
x
2
+
b
x
+
c
b
0
. Biết rằng đồ thị hàm số cắt trục hoành tại 2 điểm phân biệt đối xứng qua gốc tọa độ. Giá trị của T2(ab-c)+3 là: A. T3 B. T1 C. T2 D. T5
Đọc tiếp
Cho hàm số y = x 3 + a x 2 + b x + c b < 0 . Biết rằng đồ thị hàm số cắt trục hoành tại 2 điểm phân biệt đối xứng qua gốc tọa độ. Giá trị của T=2(ab-c)+3 là:
A. T=3
B. T=1
C. T=2
D. T=5
