Tìm giá trị của a và b:
Để hệ phương trình 3 a x - b + 1 y = 93 b x + 4 a y = - 3 có nghiệm là (x; y) = (1; -5)
cho hệ phương trình
mx-y=3
và 2x+my=9
tìm các giá trị nguyên của m để hệ phương trình có nghiệm duy nhất (x;y) sao cho giá trị của biểu thức A=3x-y nguyên
Cho hệ phương trình: a2x + y = 1 và x + y = a
a, giải hệ phương trình với a = -2
b, tìm các giá trị của a để hệ phương trình có vô số nghiệm
c, tìm a để hệ phương trình có nghiệm duy nhất (x,y) thỏa mãn x,y đều nguyên
Tìm giá trị của a và b:
Để hệ phương trình a - 2 x + 5 b y = 25 2 a x - b - 2 y = 5 có nghiệm là (x; y) = (3; -1)
Để hệ phương trình a - 2 x + 5 b y = 25 2 a x - b - 2 y = 5 có nghiệm là (x; y) = (3; -1) thì (x;y) = (3; -1) thỏa mãn hệ phương trình
Thay x = 3, y = -1 vào hệ phương trình ta được:
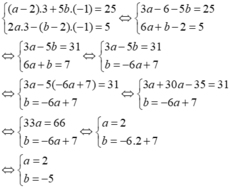
Vậy với a = 2, b = -5 thì hệ phương trình a - 2 x + 5 b y = 25 2 a x - b - 2 y = 5 có nghiệm là (x;y) = (3; -1)
Cho phương trình x\(^2\)+(4m+1)x+2(m-4)=0. Tìm giá trị của m để phương trình có hai nghiêm x\(_2\);x\(_1\)và :
a) Thỏa mãn điều kiện x\(_2\)-x\(_1\)=17
b) Biểu thức A=(x\(_1\)-x\(_2\))\(^2\)có giá trị nhỏ nhất;
c) Tìm hệ thức liên hệ giữa hai nghiệm không phụ vào m
\(\Delta=\left(4m+1\right)^2-8\left(m-4\right)=16m^2+33>0;\forall m\)
Pt luôn có 2 nghiệm pb với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-4m-1\\x_1x_2=2m-8\end{matrix}\right.\)
a. Kết hợp hệ thức Viet và đề bài: \(\left\{{}\begin{matrix}x_1+x_2=-4m-1\\x_2-x_1=17\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1=-2m-9\\x_2=-2m+8\end{matrix}\right.\)
Thế vào \(x_1x_2=2m-8\)
\(\Rightarrow\left(-2m-9\right)\left(-2m+8\right)=2m-8\)
\(\Leftrightarrow m^2-9m+20=0\Rightarrow\left[{}\begin{matrix}m=4\\m=5\end{matrix}\right.\)
b.
\(A=\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2\)
\(A=\left(4m+1\right)^2-8\left(m-4\right)\)
\(A=16m^2+33\ge33\)
\(A_{min}=33\) khi \(m=0\)
c.
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-4m-1\\x_1x_2=2m-8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=-4m-1\\2x_1x_2=4m-16\end{matrix}\right.\)
Cộng vế với vế:
\(x_1+x_2+2x_1x_2=-17\)
Đây là hệ thức liên hệ 2 nghiệm ko phụ thuộc m
Cho hệ phương trình: x+ay=2 và ax-27=1. Tìm các giá trị của a để hệ phương trình đã cho có nghiệm thỏa mãn điều kiện x>0, y<0.
Cho phương trình: x2-(2a-1)x-4a-3=0
a)CMR: phương trình luôn có nghiệm với mọi giá trị của a
b) Tìm hệ thức liên hệ giữa 2 nghiệm x1,x2 không phụ thuộc vào a
c) Tìm giá trị nhỏ nhất của biểu thức A=x12+x22
\(x^2-\left(2a-1\right)x-4a-3=0\)
\(\Delta=\left(2a-1\right)^2+4\left(4a+3\right)\)
\(=4a^2-4a+1+16a+12\)
\(=4a^2+12a+13=\left(2a+3\right)^2+4>0\)
Vì \(\Delta>0\Rightarrow\) phương trình có 2 nghiệm phân biệt với mọi a
Vì phương trình có 2 nghiệm phân biệt, áp dụng hệ thức Vi-ét, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=2a-1\\x_1.x_2=-4a-3\end{matrix}\right.\) ⇒ \(x_1.x_2+2\left(x_1+x_2\right)=-5\)
Ta có:
\(A=x_1^2+x^2_2=\left(x_1+x_2\right)^2-2x_1.x_2\)
\(=\left(2a-1\right)^2-2\left(-4a-3\right)\)
\(=4a^2-4a+1+8a+6\)
\(=\left(2a+1\right)^2+6\)
Vì \(\left(2a+1\right)^2\ge0\forall a\)
⇒\(A\ge6\)
Min A=6 <=> \(a=-\dfrac{1}{2}\)
Bài 1 Cho hệ phương trình mx+4y=10-m và x+y=4
a, giải hệ phương trình khi m= căn 2
b, giải và biện luận hệ phương trình đã cho theo tham số m
c, trong trường hợp hệ có nghiệm duy nhất (x;y) tìm các giá trị của m để:
i, y-5x=-4. ii, x<1 và y>0
Bài 2: Cho hệ phương trình 2x+3y=m và 2x-3y=6 (m là tham số không âm)
a, giải hệ phương trình với m=3
b, tìm các giá trị của m để nghiệm (x;y) của hệ phương trình thoả mãn điều kiện x>0, y>0
Cho phương trình x2 + 2(2m-1)x + 3(m2 - 1) = 0 (m là tham số)
a) Với giá trị nào của tham số m thì phương trình có nghiệm?
b) Trong trường hợp phương trình có hai nghiệm x1 và x2, dùng hệ thức Vi-ét, hãy tìm hệ thức liên hệ giữa hai nghiệm x1 và x2 của phương trình không phụ thuộc vào m.
\(x^2+2\left(2m-1\right)x+3\left(m^2-1\right)=0\)
\(a,\) Để pt có nghiệm thì \(\Delta\ge0\)
\(\Rightarrow\left[2\left(2m-1\right)\right]^2-4\left[3\left(m^2-1\right)\right]\ge0\)
\(\Rightarrow4\left(4m^2-4m+1\right)-4\left(3m^2-3\right)\ge0\)
\(\Rightarrow16m^2-16m+4-12m^2+12\ge0\)
\(\Rightarrow4m^2-16m+16\ge0\)
\(\Rightarrow\left(2m-4\right)^2\ge0\)
Vậy pt có nghiệm với mọi m.
b, Theo viét : \(\left\{{}\begin{matrix}x_1+x_2=-2\left(2m-1\right)\\x_1x_2=3\left(m^2-1\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=-4m+2\\x_1x_2=3m^2-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{-2+x_1+x_2}{4}\\x_1x_2=3\left(\dfrac{-2+x_1+x_2}{4}\right)^2-3\end{matrix}\right.\)
Vậy......
Cho hệ phương trình mx+2y=m+2 (2m-1)x+(m + 1)y = 2(m + 1)a) Giải hệ phương trình với m = 3 ? b) Tìm giá trị của m để hệ phương trình có nghiệm duy nhất , vô số nhiệm
a: \(\left\{{}\begin{matrix}mx+2y=m+2\\\left(2m-1\right)x+\left(m+1\right)y=2\left(m+1\right)\end{matrix}\right.\)
Khi m=3 thì hệ sẽ là:
3x+2y=5 và 5x+4y=8
=>x=2 và y=-1/2
b: Hệ có nghiệm duy nhất thì \(\dfrac{m}{2m-1}< >\dfrac{2}{m+1}\)
=>m^2+m<>4m-2
=>m^2-3m+2<>0
=>m<>1 và m<>2
hệ có vô số nghiệm thì \(\dfrac{m}{2m-1}=\dfrac{2}{m+1}=\dfrac{2}{2\left(m+1\right)}=\dfrac{1}{m+1}\)
=>m/2m-1=2/m+1 và 2/m+1=1/m+1(vô lý)
=>Ko có m thỏa mãn
Để hệ vô nghiệm thì m/2m-1=2/m+1<>1/m+1
=>m=2 hoặc m=1