giúp em vs

Đáp án B

Gọi   M a; a + 2 a − 2 thuộc đồ thị hàm số

  d ( M;TCD ) = a − 2

  d ( M;TCN ) = 4 a − 2

Tổng khoảng cách= a − 2 + 4 a − 2 ≥ 2 a − 2 . 4 a − 2 = 4  

Dấu bằng xảy ra khi a − 2 = 4 a − 2 ⇔ a=4 a=0  do hoành độ dương nên a=4

Vậy M(4;3)

Đáp án B

Gọi M a; a + 2 a − 2  thuộc đồ thị hàm số

  d ( M;TCD ) = a − 2

  d ( M;TCN ) = 4 a − 2

Tổng khoảng cách = a − 2 + 4 a − 2 ≥ 2 a − 2 . 4 a − 2 = 4

Dấu bằng xảy ra khi a − 2 = 4 a − 2 ⇔ a=4 a=0  do hoành độ dương nên a=4

Vậy M(4;3)

Đáp án A

Kết luận M(4;3).

\(S=\dfrac{3}{1.4}+\dfrac{3}{4.7}+...+\dfrac{3}{43.46}\\ =1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+...+\dfrac{1}{43}-\dfrac{1}{46}\\ =1-\dfrac{1}{46}\\ =\dfrac{45}{46}\\ \Rightarrow S< 1\)

Gọi ` ƯCLN(n+1 ; 2n+3)=d`

Ta có:

`n+1 vdots d => 2n+2 vdots d`

`2n+3 vdots d`

`=>(2n+3)-(2n+2) vdots d`

`=>2n+3-2n-2 vdots d`

`=>1 vdots d`

`=>ƯCLN(n+1; 2n+3)=1`

`=> (n+1)/(2n+3)` tối giản

Gọi ` ƯCLN(2n+1,3n+4)=d`

Ta có:

`2n+1 vdots d => 6n+3 vdots d`

`3n +4 vdots d =>6n+8 vdots d`

`=>(6n+8)-(6n+3) vdots d`

`=>6n+8-6n-3 vdots d`

`=>5 vdots d`

Giả sử phân số rút gọn được

`=>2n+1 vdots 5`

`=>2n+1+5 vdots 5`

`=>2n+6 vdots 5`

`=>2(n+3) vdots 5`

`=>n+3 vdots 5`

`=>n = 5k-3`

`=> n ne 5k-3`

Vậy để phân số trên tối giản thì ` n ne 5k-3`

\(a)\)Vì đths \(y=\left(2m-\frac{1}{2}\right)x\)đi qua \(A\left(-2;5\right)\)

\(\Rightarrow\)Thay \(x=-2;y=5\)vào hàm số

\(\Leftrightarrow\left(2m-\frac{1}{2}\right)\left(-2\right)=5\)

\(\Leftrightarrow2m-\frac{1}{2}=-\frac{5}{2}\)

\(\Leftrightarrow2m=-2\)

\(\Leftrightarrow m=-1\)

\(b)m=-1\)

\(\Leftrightarrow y=-\frac{5}{2}x\)

\(c)\)Lập bảng giá trị:

\(\Rightarrow\)Đths \(y=-\frac{5}{2}x\)là một đường thẳng đi qua hai điểm \(O\left(0;0\right);\left(-2;5\right)\)

Tự vẽ :<

\(d)\)Chỉ cần thành hoành độ hoặc tung độ là x hoặc y vào đths trên là tìm được cái còn lại. Khi đó tìm được tọa độ của 2 diểm trên.

a: 

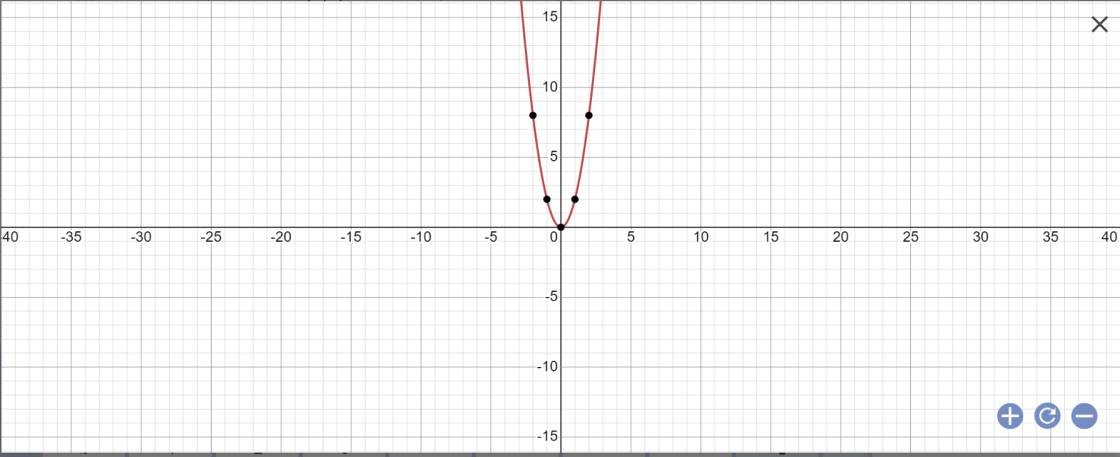
b: 2x^2=162

=>x^2=81

mà x>0

nên x=9