Cho các số phức z, w khác 0 thỏa mãn z + w ≠ 0 và 1 z + 3 w = 6 z + w . Khi đó z w bằng
A. 3
B. 1 3
C. 3
D. 1 3
Cho các số phức z, w khác 0 và thỏa mãn |z-w| = 2|z| = |w|. Phẩn thực của số phức u = z w là:
A. a = 1 4
B. a = 1
C. a = 1 8
D. a = - 1 8
Cho các số phức z, w khác 0 và thỏa mãn |z-w| = 2|z| = |w| Phẩn thực của số phức u = z w là:
![]()
![]()
![]()
![]()
Cho các số phức z, w khác 0 thỏa mãn z+w khác 0 và 1 z + 3 w = 6 z + w Khi đó z w bằng
![]()
![]()
Cho hai số phức z và w khác 0 thoả mãn|z+3w|=5|w| và |z-2wi|=|z-2w-2wi| Phần thực của số phức z/w bằng
A.1.
B.-3.
C.-1.
D.3
Cho hai số phức z, w khác 0 và thỏa mãn 3 z + 4 w = 5 z + w biết |w| = 1. Mệnh đề nào sau đây là đúng?
A . a 10 3
B . 4 10 5
C . 8 10 3
D . 8 10 5
Đáp án C.
Từ giả thiết, ta có 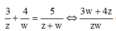
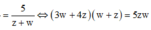
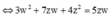
![]()
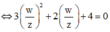
![]()
Lấy modun hai vế, ta được
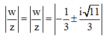
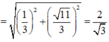
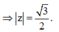
Cho hai số phức z, w khác 0 và thỏa mãn 3 z + 4 w = 5 z + w , biết w = 1. Mệnh đề nào sau đây là đúng?
A. a 10 3 .
B. 4 10 5 .
C. 8 10 3 .
D. 8 10 5 .
Đáp án C.
Từ giả thiết, ta có:
3 z + 4 w = 5 z + w ⇔ 3 w + 4 z z w = 5 z + w ⇔ 3 w + 4 z w + z = 5 z w
⇔ 3 w 2 + 7 z w + 4 z 2 = 5 z w ⇔ 3 w 2 + 2 z w + 4 z 2 = 0 ⇔ 3 w z 2 + 2 w z + 4 = 0 ⇔ w z = − 1 3 ± i 11 3 .
Lấy moodun hai vế, ta được
w z = w z = − 1 3 ± i 11 3 = 1 3 2 + 11 3 2 = 2 3 ⇒ z = 3 2 .
Cho hai số phức z,w khác 0 thoả mãn |z|=|w|= 3 2 , |z-iw|>0. Phần ảo của số phức z w bằng
A.- 4 2 9
B. -7/9.
C. 4 2 9
D. 7/9
Cho hai số phức z,w khác 0 thoả mãn |z|=|w|= 3 2 , |z-iw|>0. Phần ảo của số phức z w bằng
A.- 4 2 9
B. -7/9.
C. 4 2 9
D. 7/9
Cho z và w là các số phức thỏa mãn các điều kiện z w + 1 + i w - 1 = 0 ; w + 2 = 1 . Giá trị nhỏ nhất của biểu thức T = z - 1 - 3 i bằng
A. 2 2
B. 4 2
C. 3 2
D. 5 2