Lập phương trình chính tắc của elip trong trường hợp sau: Elip có một tiêu điểm là F 1 - 3...

Hãy tham gia nhóm Học sinh Hoc24OLM

Bạn chưa đăng nhập. Vui lòng đăng nhập để hỏi bài

Chọn lớp:

Chọn môn:

Gửi câu hỏi ẩn danh

Pham Trong Bach 21 tháng 3 2019 lúc 2:24

Lập phương trình chính tắc của elip trong trường hợp sau: Elip có một tiêu điểm là F 1 - 3 ; 0 và điểm M 1 ; 3 2 nằm trên elip...

Đọc tiếp

Lập phương trình chính tắc của elip trong trường hợp sau: Elip có một tiêu điểm là F 1 - 3 ; 0 và điểm M 1 ; 3 2 nằm trên elip.

Lớp 10 Toán

Những câu hỏi liên quan

Pham Trong Bach

1 tháng 12 2019 lúc 2:13

Lập phương trình chính tắc của elip trong trường hợp sau: Elip đi qua các điểm M(0; 3) và N(3; -12/5)

Xem chi tiết

Lớp 10 Toán

Cao Minh Tâm

1 tháng 12 2019 lúc 2:13

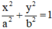
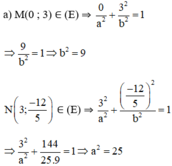
Gọi Elip cần tìm có dạng : (E) : Giải bài 3 trang 88 SGK hình học 10 | Giải toán lớp 10

Giải bài 3 trang 88 SGK hình học 10 | Giải toán lớp 10

Vậy phương trình chính tắc của elip: 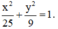Giải bài 3 trang 88 SGK hình học 10 | Giải toán lớp 10

Đúng 0

Bình luận (0)

nguyen ngoc linh

13 tháng 4 2023 lúc 22:58

viết phương trình chính tắc của elip các trường hợp sau 1. elip đi qua điểm M(0;3) và có tiêu điểm F2(5;0) 2. Elip đi qua hai điểm A(7;0), B(0;3) 3. Elip đi qua hai điểm A(0;1), N(1; căn 3 / 2)

Xem chi tiết

Lớp 10 Toán Ôn tập cuối năm môn Đại số

Nguyễn Lê Phước Thịnh CTV

13 tháng 4 2023 lúc 23:07

1: (E): x^2/a^2+y^2/b^2=1

Thay x=0 và y=3 vào (E), ta được:

3^2/b^2=1

=>b^2=9

=>b=3

F2(5;0)

=>c=5

=>$\sqrt{a^2-9}=5$

=>a^2-9=25

=>a^2=34

=>$a=\sqrt{34}$

=>x^2/34+y^2/9=1

2: Thay x=7 và y=0 vào (E), ta được:

7^2/a^2+0^2/b^2=0

=>a^2=49

=>a=7

Thay x=0 và y=3 vào (E), ta được:

0^2/a^2+3^2/b^2=1

=>b^2=9

=>b=3

=>(E): x^2/49+y^2/9=1

3: Thay x=0 và y=1 vào (E), ta được:

1/y^2=1

=>y=1

=>(E): x^2/a^2+y^2/1=1

Thay x=1 và y=căn 3/2 vào (E), ta được:

1^2/a^2+3/4=1

=>1/a^2=1/4

=>a^2=4

=>a=2

=>(E); x^2/4+y^2/1=1

Đúng 2

Bình luận (0)

Bài 3.28

SBT trang 159

9 tháng 4 2017 lúc 16:40

Viết phương trình chính tắc của elip (E) trong mỗi trường hợp sau :

a) Độ dài trục nhỏ bằng 12 và tiêu cự bằng 16

b) Một tiêu điểm là (12; 0) và điểm (13; 0) nằm trên elip

Xem chi tiết

Lớp 10 Toán §3. Phương trình elip

Nguyen Thuy Hoa

20 tháng 5 2017 lúc 9:46

a) $\left(E\right):\dfrac{x^2}{100}+\dfrac{y^2}{36}=1$

b) $\left(E\right):\dfrac{x^2}{169}+\dfrac{y^2}{25}=1$

Đúng 0

Bình luận (0)

Pham Trong Bach

19 tháng 5 2017 lúc 3:22

Elip có một tiêu điểm F(-2; 0) và tích độ dài trục lớn với trục bé bằng 12 5 . Phương trình chính tắc của elip là: A. x 2 9 + y 2 5 1. B. x 2 36 + y 2 20...

Đọc tiếp

Elip có một tiêu điểm F(-2; 0) và tích độ dài trục lớn với trục bé bằng 12 5 . Phương trình chính tắc của elip là:

A. x 2 9 + y 2 5 = 1.

B. x 2 36 + y 2 20 = 1.

C. x 2 144 + y 2 5 = 1.

D. x 2 45 + y 2 16 = 1.

Xem chi tiết

Lớp 10 Toán

Cao Minh Tâm

19 tháng 5 2017 lúc 3:23

Đáp án A

Đúng 1

Bình luận (0)

Bài 3

SGK trang 88

30 tháng 3 2017 lúc 16:33

Lập phương trình chính tắc của elip trong các trường hợp sau :

a) Elip đi qua các điểm $M\left(0;3\right)$ và $N\left(3;-\dfrac{12}{5}\right)$

b) Elip có một tiêu điểm $F_1\left(-\sqrt{3};0\right)$ và điểm $M\left(1;\dfrac{\sqrt{3}}{2}\right)$ nằm trên elip

Xem chi tiết

Lớp 10 Toán §3. Phương trình elip

Đức Minh

30 tháng 3 2017 lúc 16:55

Phương trình chính tắc của elip có dạng: $\frac{x^{2}}{a^{2}}$ + $\frac{y^{2}}{b^{2}}$ = 1

a) Elip đi qua M(0; 3):

$\frac{0^{2}}{a^{2}}$ + $\frac{3^{2}}{b^{2}}$ = 1 => b² = 9

Elip đi qua N( 3; $\frac{-12}{5}$ ):

$\frac{3^{2}}{a^{2}}$ + $\frac{(\frac{-12}{5})^{2}}{9}$ = 1 => a² = 25

Phương trình chính tắc của elip là : $\frac{x^{2}}{25}$ + $\frac{y^{2}}{9}$ = 1

b) Ta có: c = √3 => c²= 3

Elip đi qua điểm M(1; $\frac{\sqrt{3}}{2}$ )

$\frac{1}{a^{2}}$ + $\frac{(\frac{\sqrt{3}}{2})^{2}}{b^{2}}$ = 1 => $\frac{1}{a^{2}}$ + $\frac{3}{4b^{2}}$ = 1 (1)

Mặt khác: c² = a² – b²

=> 3 = a² – b²=> a² = b² + 3

Thế vào (1) ta được : $\frac{1}{b^{2}+ 3}$ + $\frac{3}{4b^{2}}$ = 1

<=> a² = 4b² + 5b²– 9 = 0 => b²= 1; b²= $\frac{-9}{4}$ ( loại)

Với b²= 1 => a² = 4

Phương trình chính tắc của elip là : $\frac{x^{2}}{4}$ + $\frac{y^{2}}{1}$ = 1.

Đúng 1

Bình luận (0)

CÔNG CHÚA THẤT LẠC

13 tháng 4 2017 lúc 21:24

Giải bài 3 trang 88 SGK hình học 10 | Giải toán lớp 10

Đúng 0

Bình luận (0)

Pham Trong Bach

1 tháng 10 2018 lúc 11:07

Cho elip (E) có một đỉnh là A( 5; 0) và có 1 tiêu điểm F1(- 4; 0). Phương trình chính tắc của elip là: A. x 2 25 + y 2 16 1. B. x 2 5 + y 2 4 1. C. ...

Đọc tiếp

Cho elip (E) có một đỉnh là A( 5; 0) và có 1 tiêu điểm F1(- 4; 0). Phương trình chính tắc của elip là:

A. x 2 25 + y 2 16 = 1.

B. x 2 5 + y 2 4 = 1.

C. x 2 25 + y 2 9 = 1.

D. x 5 + y 4 = 1.

Xem chi tiết

Lớp 10 Toán

Cao Minh Tâm

1 tháng 10 2018 lúc 11:08

Đúng 0

Bình luận (0)

camcon

21 tháng 4 2023 lúc 12:49

Lập phương trình chính tắc của Elip, biết:
Elip có hai đỉnh trên trục nhỏ cùng với hai tiêu điểm tạo thành một hình vuông có diệc tích bằng 32.

Xem chi tiết

Lớp 10 Toán Ôn tập chương III

Nguyễn Việt Lâm Giáo viên

21 tháng 4 2023 lúc 13:44

Do 2 đỉnh trên trục nhỏ và 2 tiêu điểm tạo thành hình vuông $\Rightarrow b=c$

Mặt khác diện tích hình vuông bằng 32 $\Rightarrow\dfrac{1}{2}.2b.2c=32\Rightarrow b^2=16$

$\Rightarrow a^2=b^2+c^2=2b^2=32$

Phương trình: $\dfrac{x^2}{32}+\dfrac{y^2}{16}=1$

Đúng 1

Bình luận (1)

Bài 7.22

SGK Kết nối tri thức với cuộc sống trang 56

1 tháng 10 2023 lúc 20:16

Lập phương trình chính tắc của elip đi qua hai điểm $A\left( {5;0} \right)$ và có một tiêu điểm là ${F_2}\left( {3;0} \right)$.

Xem chi tiết

Lớp 10 Toán Bài 22: Ba đường conic

Hà Quang Minh Giáo viên CTVVIP

1 tháng 10 2023 lúc 20:16

Phương trình chính tắc của elip có dạng: $\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\left( {a > b > 0} \right)$.

Elip đi qua $A\left( {5;0} \right)$ nên ta có $\frac{{{5^2}}}{{{a^2}}} + \frac{{{0^2}}}{{{b^2}}} = 1 \Leftrightarrow {a^2} = 25$

Mặt khác elip có một tiêu điểm ${F_2} = \left( {3;0} \right)$ nên ta có $c = 3$, suy ra ${b^2} = {a^2} - {c^2} = 25 - {3^2} = 16$

Vậy phương trình của elip là: $\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1$.

Đúng 0

Bình luận (0)

Pham Trong Bach

3 tháng 1 2019 lúc 7:42

Cho elip (E) có phương trình x 2 m 2 + y 2 6 m 1 . Giá trị của m để phương trình đó là phương trình chính tắc của một elip có tiêu cự bằng 8 là: A. m - 2 B. m 8 C. m - 2 hoặc m 8 D. không tồn tại m

Đọc tiếp

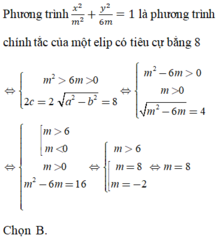
Cho elip (E) có phương trình x 2 m 2 + y 2 6 m = 1 . Giá trị của m để phương trình đó là phương trình chính tắc của một elip có tiêu cự bằng 8 là:

A. m = - 2

B. m = 8

C. m = - 2 hoặc m = 8

D. không tồn tại m

Xem chi tiết

Lớp 10 Toán

Cao Minh Tâm

3 tháng 1 2019 lúc 7:43

Đúng 0

Bình luận (0)

Câu hỏi

Khoá học trên OLM (olm.vn)