Cho hàm số y= x + m x + 1 (m là tham số thực) thỏa mãn m i n 1 ; 2 y + m a x 1 ; 2 y = 16 3
Mệnh đề nào dưới đây đúng
A. 2 < m ≤ 4
B. 0 < m ≤ 2
C. m ≤ 0
D. m > 4
Cho hàm số
f
(
x
)
=
x
3
+
m
x
2
+
n
x
-
1
với m , n là các tham số thực thỏa mãn 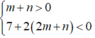 .Tìm số cực trị của hàm số
y
=
f
(
x
)
.
.Tìm số cực trị của hàm số
y
=
f
(
x
)
.
A. 2
B. 9
C. 11
D. 5
Cho hàm số y = x + m x + 1 (m là tham số thực) thỏa mãn m i n 0 ; 1 y = 3 . Mệnh đề nào dưới đây đúng?
A. 1 ≤ m < 3
B. m > 6
C. m < 1
D. 3 < m ≤ 6
Cho hàm số y = x + m x − 1 (m là tham số thực) thỏa mãn min 2 ; 4 y = 3 . Mệnh đề nào dưới đây đúng?
A. m < -1
B. 3 < m ≤ 4 .
C. m > 4
D. 1 ≤ m < 3 .
Đáp án C
Ta có: y ' = − 1 − m x − 1 2
· Trường hợp 1: nếu y ' > 0 ⇒ m < − 1 , lúc này hàm số đồng biến
⇒ min 2 ; 4 y = y 2 = 2 + m 2 − 1 = 3 ⇒ m = 1 (mâu thuẫn với m < -1) => loại
· Trường hợp 2: nếu y ' < 0 ⇒ m > − 1 , lúc này hàm số nghịch biến
⇒ min 2 ; 4 y = y 4 = 4 + m 4 − 1 = 3 ⇒ m = 5 (thỏa mãn với m > -1) => chọn
Đối chiếu 4 đáp án thì có đáp án C là thỏa mãn.
Cho hàm số y = x + m x - 1 (m là tham số thực) thỏa mãn m a x 2 ; 4 y = 2 3 . Mệnh đề nào dưới đây đúng?
A. 1 ≤ m ≤ 3
B. 3 < m ≤ 4
C. m ≤ –2
D. m > 4
Đáp án C
Phương pháp: Hàm số bậc nhất trên bậc nhất y = a x + b c x + d a d - b c ≠ 0 luôn đơn điệu trên từng khoảng xác định của nó.
TH1: Hàm số đồng biến trên [2;4] => m a x 2 ; 4 y = y ( 4 )
TH2: Hàm số nghịch biến trên [2;4] => m a x 2 ; 4 y = y ( 2 )
Cách giải: Tập xác định: D = R\{1}
Ta có: 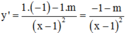
TH1: ![]()
![]() =>Hàm số đồng biến trên
=>Hàm số đồng biến trên 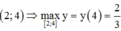
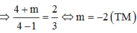
TH2: ![]()
![]() => Hàm số nghịch biến trên
=> Hàm số nghịch biến trên ![]()
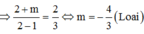
Vậy m = –2
Dựa vào các đáp án ta thấy chỉ có đáp án C thỏa mãn
Cho hàm số y = x + m x + 1 (m là tham số thực) thỏa mãn m i n [ 0 ; 1 ] y = 3 . Mệnh đề nào dưới đây đúng?
A . 3 < m ≤ 6
B . m < 1
C . m > 6
D . 1 ≤ m ≤ 3
Cho hàm số y = x + m x + 1 (m là tham số thực) thỏa mãn m i n 1 ; 2 y + m a x 1 ; 2 y = 16 3 . Mệnh đề nào dưới đây đúng?
A. 2 < m ≤ 4
B. 0 < m ≤ 2
C. m ≤ 0
D. m > 4
Cho hàm số y = m 3 x 3 + ( m - 2 ) x 2 + ( m - 1 ) x + 2 , với m là tham số thực. Tìm tất cả các giá trị thực của tham số m sao cho hàm số đạt cực đại tại điểm x 1 và đạt cực tiểu tại điểm x 2 thỏa mãn x 1 < x 2
A. 0 < m < 4 3
B. m ≤ 0
C. 5 4 < m < 4 3
D. Không tồn tại m thỏa mãn
Xét hàm số f ( t ) = 9 t 9 t + m 2 với là m tham số thực. Gọi S là tập hợp tất cả các giá trị của m sao cho f(x) + f(y) =1 với mọi số thực x, y thỏa mãn e x + y ≤ e ( x + y ) . Tìm số phần tử của S.
A. 0
B. 1
C. Vô số
D. 2
Cho hàm số y = ln 2 x - a - 2 m ln 2 x - a + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 x 2 + a 2 - 2 n - 1 - 1 log 2 x a + 1 = 0 (với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thỏa mãn M a x 1 , e 2 y = 1 . Số phần tử của S là:
A. 0
B. 1
C. 2
D. Vô số