Tìm giá trị cực tiểu y C T của hàm số y = x 4 − 2 x 2 − 3
A. y C T = 4
B. y C T = − 3
C. y C T = 3
D. y C T = − 4
Những câu hỏi liên quan
1,Tìm tất cả các giá trị của m để hàm số y2x^2 - 3mx + m - 2 trên x-1 đạt cực đại tại điểm x2.
2, Tìm tất cả các giá trị của m để hàm số y x^2 + mx +1 trên x+m đạt cực tiểu tại điểm x2.
3, Tìm tất cả các giá trị của m để hàm số yx^2 -(2m-1)x+3 trên x+2 có cực đại và cực tiểu .
4, Tìm m để hso yx^2 +m(m^2-1)x-m^4+1 trên x-m có cực đại và cực tiểu.
Mọi người giúp em với ạ . Em cảm ơn ạ !
Đọc tiếp
1,Tìm tất cả các giá trị của m để hàm số y=2x^2 - 3mx + m - 2 trên x-1 đạt cực đại tại điểm x=2. 2, Tìm tất cả các giá trị của m để hàm số y= x^2 + mx +1 trên x+m đạt cực tiểu tại điểm x=2. 3, Tìm tất cả các giá trị của m để hàm số y=x^2 -(2m-1)x+3 trên x+2 có cực đại và cực tiểu . 4, Tìm m để hso y=x^2 +m(m^2-1)x-m^4+1 trên x-m có cực đại và cực tiểu. Mọi người giúp em với ạ . Em cảm ơn ạ !
22 tháng 8 2021 lúc 20:34
Câu 3 Để đồ thị hàm số \(y=-x^4-\left(m-3\right)x^2+m+1\) có điểm cực đạt mà không có điểm cực tiểu thì tất cả giá trị thực của tham số m là
Câu 4 Cho hàm số \(y=x^4-2mx^2+m\) .Tìm tất cả các giá trị thực của m để hàm số có 3 cực trị
Bài 4: Tìm giá trị của tham số m để hàm số: a) y=mx3 +mx2 −x+1 có cực đại, cực tiểu. b) y=x4 +(m−1)x2+1 có 3 cực trị.
Cho hàm số
y
f
(
x
)
có bảng biến thiên sau: Tìm giá trị cực đại
y
C
Đ
và giá trị cực tiểu
y
C
T
của hàm số đã cho. A.
y
C
Đ
-
2
và
y
C...
Đọc tiếp
Cho hàm số y = f ( x ) có bảng biến thiên sau:
Tìm giá trị cực đại y C Đ và giá trị cực tiểu y C T của hàm số đã cho.
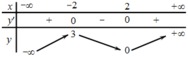
A. y C Đ = - 2 và y C T = 2 .
B. y C Đ = 3 và y C T = 0 .
C. y C Đ = 2 và y C T = 0 .
D. y C Đ = 3 và y C T = - 2 .
Tìm các giá trị của tham số m để đồ thị hàm số y =mx^4 +(2m-1)x^2 +m -2 chỉ có 1 cực đại và ko có cực tiểu.
- Với \(m=0\Rightarrow y=-x^2-2\) chỉ có cực đại (thỏa mãn)
- Với \(m\ne0\) hàm chỉ có cực đại khi:
\(\left\{{}\begin{matrix}m< 0\\m\left(2m-1\right)\ge0\end{matrix}\right.\) \(\Leftrightarrow m< 0\)
Vậy \(m\le0\)
Đúng 1
Bình luận (0)
Cho hàm số y f(x) có bảng biến thiên như hình bên dưới. Tìm giá trị cực đại và giá trị cực tiểu của hàm số đã cho A.
y
C
D
3
v
à
y
C
T
0
B.
y
C
D
2
v
à
...
Đọc tiếp
Cho hàm số y = f(x) có bảng biến thiên như hình bên dưới. Tìm giá trị cực đại và giá trị cực tiểu của hàm số đã cho
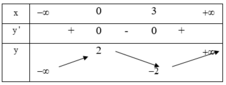
A. y C D = 3 v à y C T = 0
B. y C D = 2 v à y C T = - 2
C. y C D = - 2 v à y C T = 2
D. y C D = 0 v à y C T = 3
Cho hàm số yf(x) có bảng biến thiên như sau: Tìm giá trị cực đại
y
CD
và giá trị cực tiểu
y
CT
của hàm số đã cho A. B. C. D.
Đọc tiếp
Cho hàm số y=f(x) có bảng biến thiên như sau:
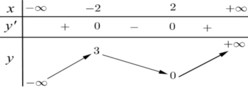
Tìm giá trị cực đại y CD và giá trị cực tiểu y CT của hàm số đã cho
A. 
B. 
C. 
D. 
Cho hàm số
y
f
(
x
)
có bảng biến thiên như sau:Tìm giá trị cực đại
y
C
Đ
và giá trị cực tiểu
y
C
T
của hàm số đã cho. A.
y
C
Đ
3
v
à
...
Đọc tiếp
Cho hàm số y = f ( x ) có bảng biến thiên như sau:
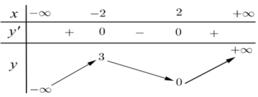
Tìm giá trị cực đại y C Đ và giá trị cực tiểu y C T của hàm số đã cho.
A. y C Đ = 3 v à y C T = - 2
B. y C Đ = 3 v à y C T = 0
C. y C Đ = 2 v à y C T = 0
D. y C Đ = - 2 v à y C T = 2
Cho hàm số yf(x) có bảng biến thiên như sau: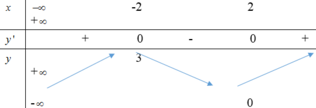Tìm giá trị cực đại yCĐ và giá trị cực tiểu yCT của hàm số đã cho A. yCĐ 3 và yCT 0 B. yCĐ 3 và yCT -2 C. yCĐ -2 và yCT 2 D. yCĐ 2 và yCT 0.
Đọc tiếp
Cho hàm số y=f(x) có bảng biến thiên như sau:
Tìm giá trị cực đại yCĐ và giá trị cực tiểu yCT của hàm số đã cho
A. yCĐ = 3 và yCT = 0
B. yCĐ = 3 và yCT = -2
C. yCĐ = -2 và yCT = 2
D. yCĐ = 2 và yCT = 0.
Tìm tất cả giá trị thực của m để hàm số y=x^4-2(m^2-m+1)x^2+m-1 có một điểm cực đại và hai điểm cực tiểu, đồng thời khoảng cách giữa hai điểm cực tiểu là ngắn nhất.
Xem chi tiết
\(y=x^4-2\left(m^2-m+1\right)x+m-1\)
\(y'=4x^3-4\left(m^2-m+1\right)x\)
\(y'=0\Leftrightarrow4x^3-4\left(m^2-m+1\right)x=0\Leftrightarrow\orbr{\begin{cases}x=0\\x=\pm\sqrt{m^2-m+1}\end{cases}}\)
Khoảng cách giữa hai điểm cực tiểu là:
\(2\sqrt{m^2-m+1}=2\sqrt{\left(m-\frac{1}{2}\right)^2+\frac{3}{4}}\ge2\sqrt{\frac{3}{4}}\)
Dấu \(=\)khi \(m-\frac{1}{2}=0\Leftrightarrow m=\frac{1}{2}\).