Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , S A ⊥ A B C D , S C tạo với mặt đáy một góc 60 ° . Tính thể tích V của khối chóp đã cho
A. V = a 3 6 6
B. V = a 3 3 6
C. V = a 3 6 3
D. V = a 3 3 3
Những câu hỏi liên quan
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SD
3
a
2
, hình chiếu vuông góc của S trên mặt phẳng (ABCD) là trung điểm của cạnh AB. Tính theo a thể tích khối chóp S.ABCD
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SD= 3 a 2 , hình chiếu vuông góc của S trên mặt phẳng (ABCD) là trung điểm của cạnh AB. Tính theo a thể tích khối chóp S.ABCD
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh hình chiếu vuông góc của S trên mặt phẳng (ABCD) là trung điểm của cạnh AB. Tính theo a thể tích khối chóp S.ABCD A.
a
3
2
B.
a
3
3
C.
a
3
4
D. ...
Đọc tiếp
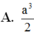
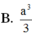
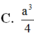
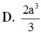
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh hình chiếu vuông góc của S trên mặt phẳng (ABCD) là trung điểm của cạnh AB. Tính theo a thể tích khối chóp S.ABCD
A. a 3 2
B. a 3 3
C. a 3 4
D. 2 a 3 3
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, hình chiếu vuông góc của S lên mặt phẳng (ABCD) trùng với trung điểm cạnh AD, cạnh SB hợp với đáy một góc
60
°
. Tính theo a thể tích V của khối chóp S.ABCD A.
a
3
15
6
B.
a
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, hình chiếu vuông góc của S lên mặt phẳng (ABCD) trùng với trung điểm cạnh AD, cạnh SB hợp với đáy một góc 60 ° . Tính theo a thể tích V của khối chóp S.ABCD
A. a 3 15 6
B. a 3 5 4
C. a 3 15 6 3
D. a 3 15 2
Cho hình chóp S.ABCD có đáy là hình thang vuông ở A và D, cạnh đáy AB a, cạnh đáy CD 2a, AD a. Hình chiếu vuông góc của S lên đáy trùng với trung điểm CD. Biết rằng diện tích mặt bên (SBC) bằng
3
a
2
2
. Thể tích của hình chóp S.ABCD bằng:A.
a
3
B.
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang vuông ở A và D, cạnh đáy AB = a, cạnh đáy CD = 2a, AD = a. Hình chiếu vuông góc của S lên đáy trùng với trung điểm CD. Biết rằng diện tích mặt bên (SBC) bằng 3 a 2 2 . Thể tích của hình chóp S.ABCD bằng:
A. a 3 B. 3 a 3 2
C. 3 a 3 D. 3 2 a 3
Chọn A.
Gọi H là trung điểm của CD, M là trung điểm của BC. Khi đó HM ⊥ BC, SM ⊥ BC. Dễ thấy tam giác HBC vuông cân ở H, do đó tính được BC, SM. Từ đó tính được SH.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB vuông tại S và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối cầu ngoại tiếp hình chóp S.ABCD bằng A.
πa
3
3
B.
2
πa
3
3
C.
πa
3
6
D....
Đọc tiếp
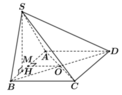
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB vuông tại S và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối cầu ngoại tiếp hình chóp S.ABCD bằng
A. πa 3 3
B. 2 πa 3 3
C. πa 3 6
D. 11 11 πa 3 162
Gọi M là trung điểm AB, do tam giác SAB vuông tại S nên MS = MA = MB
Gọi H là hình chiếu của S trên AB. Từ giả thiết suy ra 
Ta có 
nên là trục của tam giác SAB, suy ra OA = OB = OS (2)
Từ (1) và (2) ta có OS = OA = OB = OC = OD.
Vậy O là tâm mặt cầu ngoại tiếp khối chóp S.ABCD bán kính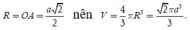 
Chọn B.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, SA a
3
. Tính thể tích hình chóp S.ABCD. A.
a
3
3
B.
a
3
3
3
C.
a
3
3
D. 3
a...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, SA = a 3 . Tính thể tích hình chóp S.ABCD.
A. a 3 3
B. a 3 3 3
C. a 3 3
D. 3 a 3 3
Phương pháp:
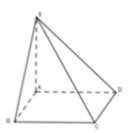
Thể tích khối chóp có chiều cao h và diện tích đáy S là 
Cách giải:
Diện tích đáy 
Thể tích khối chóp là
Chọn B.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a,
SD
13
2
. Hình chiếu của S lên mặt phẳng (ABCD) là trung điểm H của AB. Thể tích khối chóp S.ABCD là: A.
a
3
2
3
B.
a
3
12
C.
a...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SD = 13 2 . Hình chiếu của S lên mặt phẳng (ABCD) là trung điểm H của AB. Thể tích khối chóp S.ABCD là:
A. a 3 2 3
B. a 3 12
C. a 3 3
D. 2 a 3 3
Đáp án A
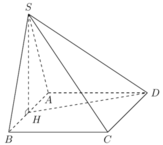
Ta có tam giác AHD vuông tại A, suy ra
H D = A H 2 + D H 2 = a 2 4 + a 2 = a 5 2
Tam giác SHD vuông tại H, suy ra:
S
H
=
S
D
2
-
H
D
2
=
13
a
2
4
-
5
a
2
4
=
a
2
Vậy V S . A B C D = a 3 2 3
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a; hình chiếu vuông góc của S lên mặt phẳng (ABCD) trùng với trung điểm của cạnh AD; cạnh bên SB hợp với đáy một góc
60
o
Tính theo a thể tích V của khối chóp S.ABCD.
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a; hình chiếu vuông góc của S lên mặt phẳng (ABCD) trùng với trung điểm của cạnh AD; cạnh bên SB hợp với đáy một góc 60 o Tính theo a thể tích V của khối chóp S.ABCD.
SGK Cánh Diều
14 tháng 8 2023 lúc 0:01
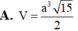
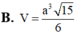
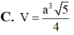
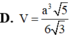
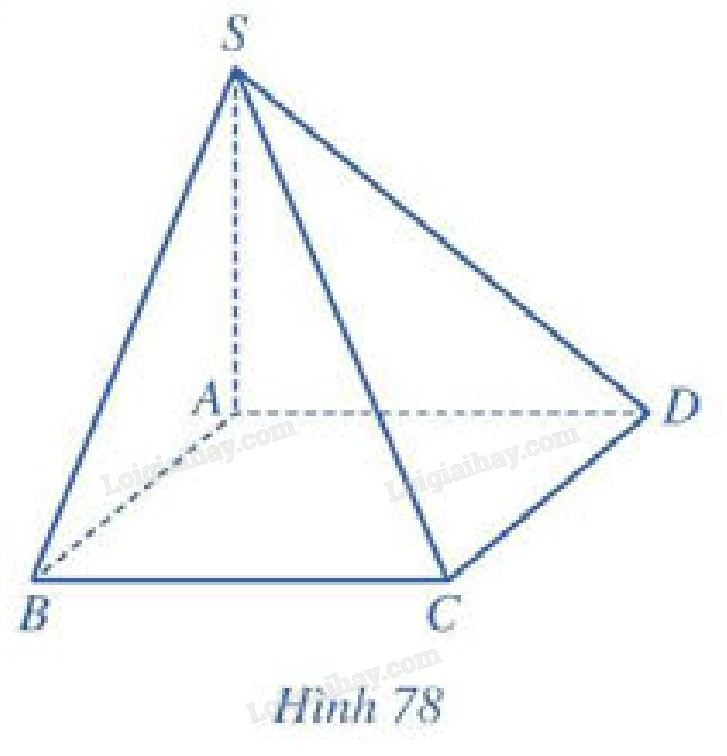
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\), đáy \(ABCD\) là hình vuông cạnh \(a\), \(SA = a\) (Hình 78).
a) Tính khoảng cách từ điểm \(S\) đến đường thẳng \(C{\rm{D}}\).
b) Tính khoảng cách từ điểm \(D\) đến mặt phẳng \(\left( {SAB} \right)\).
c) Tính khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {SCD} \right)\).
a) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot C{\rm{D}}\)
\(ABCD\) là hình vuông \( \Rightarrow A{\rm{D}} \bot C{\rm{D}}\)
\(\begin{array}{l} \Rightarrow C{\rm{D}} \bot \left( {SA{\rm{D}}} \right) \Rightarrow C{\rm{D}} \bot S{\rm{D}}\\ \Rightarrow d\left( {S,C{\rm{D}}} \right) = S{\rm{D}} = \sqrt {S{A^2} + A{{\rm{D}}^2}} = a\sqrt 2 \end{array}\)
b) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot A{\rm{D}}\)
\(ABCD\) là hình vuông \( \Rightarrow A{\rm{B}} \bot A{\rm{D}}\)
\( \Rightarrow A{\rm{D}} \bot \left( {SA{\rm{B}}} \right) \Rightarrow d\left( {D,\left( {SAB} \right)} \right) = A{\rm{D}} = a\)
c) Kẻ \(AH \bot S{\rm{D}}\left( {H \in S{\rm{D}}} \right)\).
\(C{\rm{D}} \bot \left( {SA{\rm{D}}} \right) \Rightarrow C{\rm{D}} \bot AH\)
\( \Rightarrow AH \bot \left( {SC{\rm{D}}} \right) \Rightarrow d\left( {A,\left( {SC{\rm{D}}} \right)} \right) = AH\)
Tam giác \(SAD\) vuông tại \(A\) có đường cao \(AH\)
\( \Rightarrow AH = \frac{{SA.A{\rm{D}}}}{{S{\rm{D}}}} = \frac{{a\sqrt 2 }}{2}\)
Vậy \(d\left( {A,\left( {SC{\rm{D}}} \right)} \right) = \frac{{a\sqrt 2 }}{2}\).
Đúng 1
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a,
S
A
2
a
2
, tam giác SAC vuông tại S và nằm trong mặt phẳng vuông góc với (ABCD). Tính theo a thể tích V của khối chóp S.ABCD. A.
V
6
a
3
12
B.
V...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, S A = 2 a 2 , tam giác SAC vuông tại S và nằm trong mặt phẳng vuông góc với (ABCD). Tính theo a thể tích V của khối chóp S.ABCD.
A. V = 6 a 3 12
B. V = 6 a 3 3
C. V = 6 a 3 4
D. V = 6 a 3 6
