Biết rằng bất phương trình m x + 1 − x 2 + 1 ≤ 2 x 2 − x 4 + x 2 + 1 − x 2 + 2 có nghiệm khi và chỉ khi m ∈ − ∞ ; a 2 + b với a , b ∈ ℤ . Tính giá trị của T = a + b .
A. T = 0
B. T = 1
C. T = 2
D. T = 3
Những câu hỏi liên quan
Với m là tham số thực dương khác 1. Hãy tìm tập nghiêm S của bất phương trình
log
m
2
x
2
+
x
+
3
≤
log
m
3
x
2
−
x
.
Biết rằ...
Đọc tiếp
Với m là tham số thực dương khác 1. Hãy tìm tập nghiêm S của bất phương trình log m 2 x 2 + x + 3 ≤ log m 3 x 2 − x . Biết rằng x = 1 là một nghiệm của bất phương trình
A. S = − 2 ; 0 ∪ 1 3 ; 3
B. S = − 1 ; 0 ∪ 1 3 ; 2
C. S = − 1 ; 0 ∪ 1 3 ; 3
D. S = − 1 ; 0 ∪ 1 ; 3
Đáp án C
Vì x = 1 là một nghiệm của bất phương trình
⇒ log m 4 ≤ log m 2 ⇔ log m 2 ≤ 0 ⇔ m ∈ 0 ; 1 .
Khi đó, bất phương trình
log m 2 x 2 + x + 3 ≤ log m 3 x 2 − x ⇔ 3 x 2 − x > 0 2 x 2 + x + 3 ≥ 3 x 2 − x ⇔ − 1 ≤ x < 0 1 3 < x ≤ 3 .
Đúng 0
Bình luận (0)
Với m là tham số thực dương khác 1. Hãy tìm tập nghiêm S của bất phương trình logm(2x2 + x + 3)
≤
logm(3x2 - x). Biết rằng x 1 là một nghiệm của bất phương trình.
Đọc tiếp
Với m là tham số thực dương khác 1. Hãy tìm tập nghiêm S của bất phương trình logm(2x2 + x + 3) ≤ logm(3x2 - x). Biết rằng x = 1 là một nghiệm của bất phương trình.
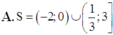
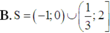
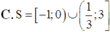
Đáp án C
Vì x = 1 là một nghiệm của bất phương trình
Khi đó, bất phương trình
Đúng 0
Bình luận (0)
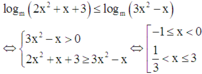
Bài 1: Cho bất phương trình \(4\sqrt{\left(x+1\right)\left(3-x\right)}\le x^2-2x+m-3\). Xác định m để bất phương trình nghiệm \(\forall x\in[-1;3]\)
Bài 2: Cho bất phương trình \(x^2-6x+\sqrt{-x^2+6x-8}+m-1\ge0\). Xác định m để bất phương trình nghiệm đúng \(\forall x\in[2;4]\)
Biết rằng m là một số dương để bất phương trình
m
x
≥
2
x
+
1
nghiệm đúng với
∀
x
∈
R
. Giá trị lớn nhất của hàm số
y
x
+
ln
m
x
-
1
,
x
∈
2...
Đọc tiếp
Biết rằng m là một số dương để bất phương trình m x ≥ 2 x + 1 nghiệm đúng với ∀ x ∈ R . Giá trị lớn nhất của hàm số y = x + ln m x - 1 , x ∈ 2 ; 4 thuộc đoạn nào dưới đây
Biết rằng m là một số dương để bất phương trình
m
x
≥
2
x
+
1
nghiệm đúng với
∀
x
∈
ℝ
. Giá trị lớn nhất của hàm số
y
x
+
ln
m
x
-
1
,
x
∈...
Đọc tiếp
Biết rằng m là một số dương để bất phương trình m x ≥ 2 x + 1 nghiệm đúng với ∀ x ∈ ℝ . Giá trị lớn nhất của hàm số y = x + ln m x - 1 , x ∈ 2 ; 4 thuộc đoạn nào dưới đây
A. [1;2]
B. [2,5;5]
C. [5;6]
D. [7;9]
Cho bất phương trình
2
log
3
2
(
3
x
)
-
2
m
log
3
x
+
3
log
2
x...
Đọc tiếp
Cho bất phương trình 2 log 3 2 ( 3 x ) - 2 m log 3 x + 3 log 2 x ( log 3 x + 2 - 2 m ) log 3 x ≤ 2 Biết rằng bất phương trình có đúng 74 nghiệm nguyên x ∈ 8 ; 2018 Giá trị nguyên của tham số m thỏa mãn bài toán nằm trong khoảng
A. (0;4)
B. (4;7)
C. (7;15)
D. (15;70)
Cho bất phương trình x² -m(x-1) ≥ 0 . Tìm m để bất phương trình đúng với ∀x∈R
\(x^2-m\left(x-1\right)\ge0\Leftrightarrow x^2-mx+m\ge0\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=1>0\\\Delta\le0\end{matrix}\right.\Leftrightarrow m^2-4m\le0\Leftrightarrow0\le m\le4\)
Đúng 0
Bình luận (0)
(m²-1)x²-x+3>0
Tìm m để bất phương trình sau là bất phương trình bậc nhất 1 ẩn
-Để phương trình trên là bất phương trình bậc nhất 1 ẩn thì:
\(m^2-1=0\)
\(\Leftrightarrow\left(m-1\right)\left(m+1\right)=0\)
\(\Leftrightarrow m=1\) hay \(m=-1\)
Đúng 1
Bình luận (0)
Xét xem x -3 là nghiệm của bất phương trình nào trong hai bất phương trình sau 3x + 1 x + 3 (1) và
(
3
x
+
1
)
2
(
x
+
3
)
2...
Đọc tiếp
Xét xem x = -3 là nghiệm của bất phương trình nào trong hai bất phương trình sau 3x + 1 < x + 3 (1) và ( 3 x + 1 ) 2 < ( x + 3 ) 2 (2)
Từ đó suy ra rằng phép bình phương hai vế một bất phương trình không phải là phép biến đổi tương đương.
Thử trực tiếp ta thấy ngay x = -3 là nghiệm của bất phương trình (1) nhưng không là nghiệm bất phương trình (2), vì vậy (1) và (2) không tương đương do đó phép bình phương hai vế một bất phương trình không phải là phép biến đổi tương đương.
Đúng 0
Bình luận (0)
Cho bất phương trình: (x+2m)(x+1)>0. Tìm m để tập nghiệm của bất phương trình chứa (1;+∞)
- Với \(m=\dfrac{1}{2}\Rightarrow\left(x+1\right)^2>0\) có tập nghiệm \(R\backslash\left\{-1\right\}\) thỏa mãn
- Với \(m>\dfrac{1}{2}\) BPT có nghiệm: \(\left\{{}\begin{matrix}x>-1\\x< -2m\end{matrix}\right.\) hay \(D=\left(-\infty;-2m\right)\cup\left(-1;+\infty\right)\)
Thỏa mãn do \(\left(1;+\infty\right)\subset\left(-1;+\infty\right)\)
- Với \(m< \dfrac{1}{2}\) BPT có nghiệm: \(\left\{{}\begin{matrix}x>-2m\\x< -1\end{matrix}\right.\) hay \(D=\left(-\infty;-1\right)\cup\left(-2m;+\infty\right)\)
Tập nghiệm của BPT chứa \(\left(1;+\infty\right)\) khi:
\(-2m\le1\Rightarrow m\ge-\dfrac{1}{2}\Rightarrow-\dfrac{1}{2}\le m< \dfrac{1}{2}\)
Kết hợp lại ta được: \(m\ge-\dfrac{1}{2}\)
Đúng 1
Bình luận (0)