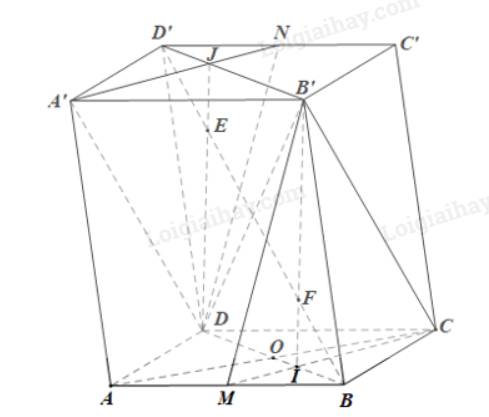
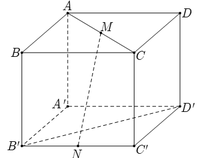
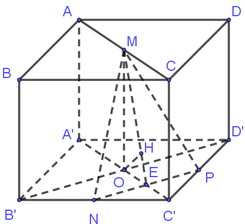
Cho hình hộp A B C D . A ' B ' C ' D ' . Gọi M, N, P lần lượt là trung điểm của A A ' , B C , C D . Mặt phẳng M N P chia khối hộp thành hai phần có thể tích là V 1 , V 2 . Gọi V 1 là thể tích phần chứa điểm C. Tỉ số V 1 V 2 bằng
A. 119 25
B. 3 4
C. 113 24
D. 119 425