Hàm số f ( x ) = 10 x 2 - 2 x có đạo hàm
A. f ' ( x ) = ( 2 x - 2 ) ln 10
B. f ' ( x ) = ( x 2 - 2 x ) 10 x 2 - 2 x - 1
C. f ' ( x ) = 2 ( x - 2 ) 10 x 2 - 2 x
D. f ' ( x ) = ( 2 x - 2 ) 10 x 2 - 2 x ln 10
Những câu hỏi liên quan
Đạo hàm y 0 −3x 2 + 6x + m − 1. Hàm số đã cho đồng biến trên khoảng (0; 3) khi và chỉ khi y 0 0, ∀x ∈ (0; 3). Hay −3x 2 + 6x + m − 1 0, ∀x ∈ (0; 3) ⇔ m 3x 2 − 6x + 1, ∀x ∈ (0; 3) (∗). Xét hàm số f(x) 3x 2 − 6x + 1 trên đoạn [0; 3] có f 0 (x) 6x − 6; f 0 (x) 0 ⇔ x 1. Khi đó f(0) 1, f(3) 10, f(1) −2, suy ra max [0;3] f(x) f(3) 10. Do đó (∗) ⇔ m max [0;3] f(x) ⇔ m 10. Vậy với m 10 thì hàm số đã cho đồng biến trên khoảng (0; 3).
Đọc tiếp
Đạo hàm y 0 = −3x 2 + 6x + m − 1. Hàm số đã cho đồng biến trên khoảng (0; 3) khi và chỉ khi y 0 > 0, ∀x ∈ (0; 3). Hay −3x 2 + 6x + m − 1 > 0, ∀x ∈ (0; 3) ⇔ m > 3x 2 − 6x + 1, ∀x ∈ (0; 3) (∗). Xét hàm số f(x) = 3x 2 − 6x + 1 trên đoạn [0; 3] có f 0 (x) = 6x − 6; f 0 (x) = 0 ⇔ x = 1. Khi đó f(0) = 1, f(3) = 10, f(1) = −2, suy ra max [0;3] f(x) = f(3) = 10. Do đó (∗) ⇔ m > max [0;3] f(x) ⇔ m > 10. Vậy với m > 10 thì hàm số đã cho đồng biến trên khoảng (0; 3).
Cho hàm số y f(x) có đạo hàm liên tục trên R đồ thị hàm số y f’(x) như hình vẽ.Biết f(2) –6, f(–4) –10 và hàm số g(x) f(x)+
x
2
2
, g(x) có ba điểm cực trị. Phương trình g(x) 0? A. Có đúng 2 nghiệm B. Vô nghiệm C. Có đúng 3 nghiệm D. Có đúng 4 nghiệm
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm liên tục trên R đồ thị hàm số y = f’(x) như hình vẽ.
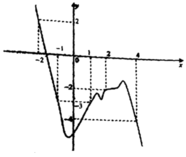
Biết f(2) = –6, f(–4) = –10 và hàm số g(x) = f(x)+ x 2 2 , g(x) có ba điểm cực trị.
Phương trình g(x) = 0?
A. Có đúng 2 nghiệm
B. Vô nghiệm
C. Có đúng 3 nghiệm
D. Có đúng 4 nghiệm
Đáp án B
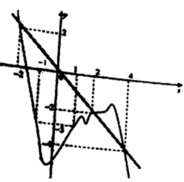
Phương pháp: Lập bảng biến thiên của g(x) và đánh giá số giao điểm của đồ thị hàm số y = g(x) và trục hoành.
Cách giải: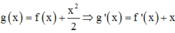 
Xét giao điểm của đồ thị hàm sốy = f’(x) và đường thẳng y = -x ta thấy, hai đồ thị cắt nhau tại ba điểm có hoành độ là: -2;2;4 tương ứng với 3 điểm cực trị của y = g(x).
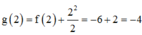
Bảng biến thiên:
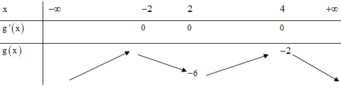
Dựa vào bảng biến thiên ta thấy 
=> phương trình g(x) = 0 không có nghiệm 
Đúng 0
Bình luận (0)
Cho hàm số y=f(x)=(5-3a)x+2
a/ Với giá trị nào của a thì hàm số đồng biến
b/ Tính f(2), biết f(-2)=10
Xem chi tiết
a) Để hàm số đồng biến \(\Leftrightarrow5-3a>0\) \(\Leftrightarrow a< \dfrac{5}{3}\)
b) Ta có: \(f\left(-2\right)=10\) \(\Rightarrow\left(5-3a\right)\cdot\left(-2\right)+2=10\) \(\Rightarrow a=3\)
\(\Rightarrow f\left(2\right)=\left(5-3\cdot3\right)\cdot2+2=-6\)
Đúng 0
Bình luận (0)
Cho hàm số y=f(x)=I3x-1I
a) Tính f(-2);f(2);f(\(\dfrac{-1}{4}\))
b)Tìm x biết f(x)=10;f(x)=-3
a) Ta có:
\(f\left(-2\right)=\left|3\cdot-2-1\right|=\left|-6-1\right|=\left|-7\right|=7\)
\(f\left(2\right)=\left|3\cdot2-1\right|=\left|6-1\right|=5\)
\(f\left(-\dfrac{1}{4}\right)=\left|3\cdot-\dfrac{1}{4}-1\right|=\left|-\dfrac{3}{4}-1\right|=\left|-\dfrac{7}{4}\right|=\dfrac{7}{4}\)
b) Ta có:
\(f\left(x\right)=10\)
\(\Rightarrow\left|3x-1\right|=10\)
Với \(x\ge\dfrac{1}{3}\Rightarrow3x-1=10\)
\(\Rightarrow3x=11\Rightarrow x=\dfrac{11}{3}\left(tm\right)\)
Với \(x< \dfrac{1}{3}\Rightarrow3x-1=-10\)
\(\Rightarrow3x=-9\Rightarrow x=-3\left(tm\right)\)
_______
\(f\left(x\right)=-3\)
\(\Rightarrow\left|3x-1\right|=-3\)
Mà: \(\left|3x-1\right|\ge0\forall x\) và \(-3< 0\)
\(\Rightarrow\left|3x-1\right|=-3\) (vô lý)
\(\Rightarrow\) không có x thỏa mãn
Đúng 1
Bình luận (0)
cho hàm số y = f(x)=x mũ 2 + 4 a) Tính f(1/-2);f(5) b) tìm x khi biết f(x)=10
Cho hàm số x thỏa mãn 2.f(x)-x.f(-x)=x + 10 với mọi x . Vậy f(2) bằng?
ap dung ta co:
f(2)=2f(2)-2f(-2)=12 (1)
f(-2)=2f(-2)+2f(2)=8 (2)
cong tung ve cua (1) va(2) ta co:
4f(2)=20
=>f(2)=5
Đúng 1
Bình luận (0)
Cho hàm số y f(x) có đạo hàm liên tục trên [1;2] thỏa mãn
∫
1
2
f
(
x
)
d
x
10
và
∫
1
2
f
(
x
)
f
(
x
)...
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm liên tục trên [1;2] thỏa mãn ∫ 1 2 f ' ( x ) d x = 10 và ∫ 1 2 f ' ( x ) f ( x ) d x = ln 2 . Biết rằng f(x)>0. Tính f(2)
A. f(2) = 10
B. f(2) = -20
C. f(2) = -10
D. f(2) = 20
Cho hàm số y=f(x) thỏa mãn: 2.f(x)-x.f(x)=x+10(với mọi x thuộc R).Tính f(2).
Tìm giá trị thực của m để hàm số F(x) x3 – (2m – 3)2 – 4x + 10 là một nguyên hàm của hàm số f(x) 3x2 – 12x – 4 với mọi
x
∈
ℝ
A.
m
3
2
B.
m
-
9
2
C.
m
9
2
D.
m...
Đọc tiếp
Tìm giá trị thực của m để hàm số F(x) = x3 – (2m – 3)2 – 4x + 10 là một nguyên hàm của hàm số f(x) = 3x2 – 12x – 4 với mọi x ∈ ℝ
A. m = 3 2
B. m = - 9 2
C. m = 9 2
D. m = 9
Cho hàm số y = f(x) = 10.x 2 – 5. Tính f(-3)
Xem thêm câu trả lời